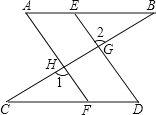
【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠B=40°,求∠AGD的度数.

参考答案:
【答案】(1)DG∥BC,理由见解析;(2)∠AGD=70°.
【解析】
(1)根据平行线的判定推出CD∥EF,根据平行线的性质得出∠1=∠BCD,求出∠2=∠BCD,根据平行线的判定得出即可;
(2)根据三角形内角和定理求出∠ACB,根据平行线的性质得出∠AGD=∠ACB,即可得出答案.
解:(1)DG∥BC,
理由是:∵CD⊥AB,EF⊥AB,
∴∠CDB=∠EFB=90°,
∴CD∥EF,
∴∠1=∠BCD,
∵∠1=∠2,
∴∠2=∠BCD,
∴DG∥BC;
(2)∵∠A=70°,∠B=40°,
∴∠ACB=180°﹣∠B﹣∠A=70°,
∵DG∥BC,
∴∠AGD=∠ACB=70°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,BC>AD,∠B与∠C互余, 将AB,CD分别平移到EF和EG的位置,则△EFG为________三角形,若AD=2cm,BC=8cm,则FG=____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC、△ADE均为是顶角为42的等腰三角形,BC和DE分别是底边,图中△_________与△___________,可以通过以点________为旋转中心,旋转角度为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣
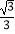 x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限内作等边△ABC.
x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限内作等边△ABC.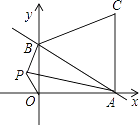
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(a, ),请用含a的式子表示四边形ABPO的面积,并求出当△ABP的面积与△ABC的面积相等时a的值.
),请用含a的式子表示四边形ABPO的面积,并求出当△ABP的面积与△ABC的面积相等时a的值. -
科目: 来源: 题型:
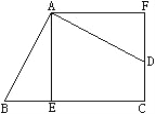
查看答案和解析>>【题目】如图,四边形ABCD的∠BAD=∠C=90,AB=AD,AE⊥BC于E,
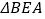 旋转后能与
旋转后能与 重合.
重合.(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)若AE=5㎝,求四边形AECF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题提出
(1)如图①,已知△ABC,请画出△ABC关于直线AC对称的三角形.
(2)问题探究
如图②,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在边BC、CD上分别存在点G、H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.
(3)如图③,有一矩形板材ABCD,AB=3米,AD=6米,现想从此板材中裁出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,EF=FG= 米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积;若不能,请说明理由.
米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:E、F分别是AB和CD上的点,DE、AF分别交BC于点G、H, AB∥CD,∠A=∠D,试说明:(1)AF∥ED;(2)∠BED=∠A;(3) ∠1=∠2.
相关试题

