【题目】如图,已知二次函数![]() (b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(1)求该二次函数的解析式及点M的坐标;
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;
(3)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).
参考答案:
【答案】(1)![]() ,M(1,5);(2)2<m<4;(3)P1(
,M(1,5);(2)2<m<4;(3)P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ),P3(3,1),P4(﹣3,7).
),P3(3,1),P4(﹣3,7).
【解析】
试题分析:(1)将点A、点C的坐标代入函数解析式,即可求出b、c的值,通过配方法得到点M的坐标;
(2)点M是沿着对称轴直线x=1向下平移的,可先求出直线AC的解析式,将x=1代入求出点M在向下平移时与AC、AB相交时y的值,即可得到m的取值范围;
(3)由题意分析可得∠MCP=90°,则若△PCM与△BCD相似,则要进行分类讨论,分成△PCM∽△BDC或△PCM∽△CDB两种,然后利用边的对应比值求出点坐标.
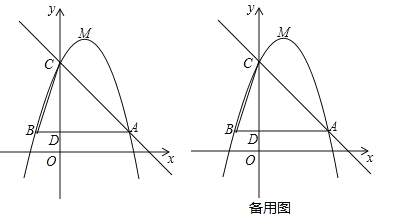
试题解析:(1)把点A(3,1),点C(0,4)代入二次函数![]() ,得:
,得: 解得:
解得:![]() ,∴二次函数解析式为
,∴二次函数解析式为![]() ,配方得
,配方得![]() ,∴点M的坐标为(1,5);
,∴点M的坐标为(1,5);
(2)设直线AC解析式为y=kx+b,把点A(3,1),C(0,4)代入得:![]() 解得:
解得:![]() ,∴直线AC的解析式为y=﹣x+4,如图所示,对称轴直线x=1与△ABC两边分别交于点E、点F.
,∴直线AC的解析式为y=﹣x+4,如图所示,对称轴直线x=1与△ABC两边分别交于点E、点F.
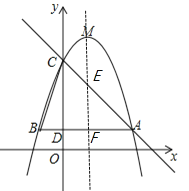
把x=1代入直线AC解析式y=﹣x+4解得y=3,则点E坐标为(1,3),点F坐标为(1,1),∴1<5﹣m<3,解得2<m<4;
(3)连接MC,作MG⊥y轴并延长交AC于点N,则点G坐标为(0,5).
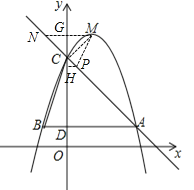
∵MG=1,GC=5﹣4=1,∴MC=![]() =
=![]() =
=![]() ,把y=5代入y=﹣x+4解得x=﹣1,则点N坐标为(﹣1,5),∵NG=GC,GM=GC,∴∠NCG=∠GCM=45°,∴∠NCM=90°,由此可知,若点P在AC上,则∠MCP=90°,则点D与点C必为相似三角形对应点.
,把y=5代入y=﹣x+4解得x=﹣1,则点N坐标为(﹣1,5),∵NG=GC,GM=GC,∴∠NCG=∠GCM=45°,∴∠NCM=90°,由此可知,若点P在AC上,则∠MCP=90°,则点D与点C必为相似三角形对应点.
①若有△PCM∽△BDC,则有![]() ,∵BD=1,CD=3,∴CP=
,∵BD=1,CD=3,∴CP=![]() =
=![]() =
=![]() ,∵CD=DA=3,∴∠DCA=45°,若点P在y轴右侧,作PH⊥y轴,∵∠PCH=45°,CP=
,∵CD=DA=3,∴∠DCA=45°,若点P在y轴右侧,作PH⊥y轴,∵∠PCH=45°,CP=![]() ,span>∴PH=
,span>∴PH=![]() =
=![]() ,把x=
,把x=![]() 代入y=﹣x+4,解得y=
代入y=﹣x+4,解得y=![]() ,∴P1(
,∴P1(![]() ,
,![]() );
);
同理可得,若点P在y轴左侧,则把x=![]() 代入y=﹣x+4,解得y=
代入y=﹣x+4,解得y=![]() ,∴P2(
,∴P2(![]() ,
,![]() );
);
②若有△PCM∽△CDB,则有![]() ,∴CP=
,∴CP=![]() =
=![]() ,∴PH=
,∴PH=![]() =3;
=3;
若点P在y轴右侧,把x=3代入y=﹣x+4,解得y=1;
若点P在y轴左侧,把x=﹣3代入y=﹣x+4,解得y=7
∴P3(3,1);P4(﹣3,7),∴所有符合题意得点P坐标有4个,分别为P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ),P3(3,1),P4(﹣3,7).
),P3(3,1),P4(﹣3,7).
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节前夕,某商店根据市场调查,用1320元购进第一批盒装粽子,上市后很快售完,接着又用2880元购进第二批这种盒装粽子,已知第二批所购的粽子盒数是第一批所购粽子盒数的2倍,且每盒粽子的进价比第一批的进价多1元.
(1)第一批盒装粽子购进多少盒?
(2)若两批粽子按相同的标价销售,最后剩下50盒按八折优惠售出,如果两批粽子全部售出后利润不低于25%(不考虑其他因素),那么每盒粽子的标价至少是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:C是线段AB所在平面内任意一点,分别以AC、BC为边,在AB同侧作等边三角形ACE和BCD,联结AD、BE交于点P.

(1)如图1,当点C在线段AB上移动时,线段AD与BE的数量关系是: .
(2)如图2,当点C在直线AB外,且∠ACB<120°,上面的结论是否还成立?若成立请证明,不成立说明理由.
(3)在(2)的条件下,∠APE大小是否随着∠ACB的大小发生变化而发生变化,若变化写出变化规律,若不变,请求出∠APE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】琪琪想了解全市八年级学生每天写作业的时间,她对某校八年级(4)班全体学生每天写作业的时间进行了一次调查.
(1)调查的问题是什么?
(2)调查的范围有多大?用了哪种调查方式?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠1=∠2,求证:∠3+∠4=180°.
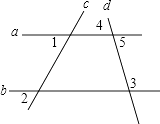
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在元旦为好友小李制作了一个(如图)正方体礼品盒,六面上各有一字,连起来就是“祝你学年快乐”,其中“祝”的对面是“新”,“快”的对面是“乐”,则它的平面展开图可能是( )
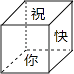
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…,若m3分裂后,其中有一个奇数是123,则m的值是( )
A.9
B.10
C.11
D.12
相关试题

