【题目】已知:如图,∠1=∠2,求证:∠3+∠4=180°.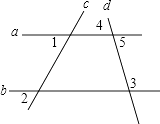
参考答案:
【答案】解:∵∠1=∠2,
∴a∥b,
∴∠3+∠5=180°,
∵∠4=∠5,
∴∠3+∠4=180°.
【解析】首先依据同位角相等两直线平行可得到a∥b,然后再依据平行线的性质可得到∠3+∠5=180°,然后通过等量代换可得到∠3+∠4=180°.
【考点精析】本题主要考查了对顶角和邻补角和平行线的判定与性质的相关知识点,需要掌握两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:C是线段AB所在平面内任意一点,分别以AC、BC为边,在AB同侧作等边三角形ACE和BCD,联结AD、BE交于点P.

(1)如图1,当点C在线段AB上移动时,线段AD与BE的数量关系是: .
(2)如图2,当点C在直线AB外,且∠ACB<120°,上面的结论是否还成立?若成立请证明,不成立说明理由.
(3)在(2)的条件下,∠APE大小是否随着∠ACB的大小发生变化而发生变化,若变化写出变化规律,若不变,请求出∠APE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】琪琪想了解全市八年级学生每天写作业的时间,她对某校八年级(4)班全体学生每天写作业的时间进行了一次调查.
(1)调查的问题是什么?
(2)调查的范围有多大?用了哪种调查方式?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
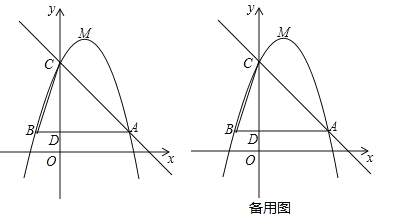
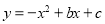 (b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.(1)求该二次函数的解析式及点M的坐标;
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;
(3)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).
-
科目: 来源: 题型:
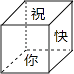
查看答案和解析>>【题目】小明在元旦为好友小李制作了一个(如图)正方体礼品盒,六面上各有一字,连起来就是“祝你学年快乐”,其中“祝”的对面是“新”,“快”的对面是“乐”,则它的平面展开图可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…,若m3分裂后,其中有一个奇数是123,则m的值是( )
A.9
B.10
C.11
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+b=3,ab=2,则a2+b2的值为( )
A.3
B.4
C.5
D.6
相关试题

