【题目】已知:如图,二次函数图象的顶点坐标为C(1,﹣2),直线y=kx+m的图象与该二次函数的图象交于A、B两点,其中A点坐标为(3,0),B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这个二次函数的图象交于点E.
(1)求这个二次函数的解析式;
(2)设点P的横坐标为x,求线段PE的长(用含x 的代数式表示);
(3)点D为直线AB与这个二次函数图象对称轴的交点,若以点P、E、D为顶点的三角形与△AOB相似,请求出P点的坐标.

参考答案:
【答案】(1)y=![]() (x﹣1)2﹣2;(2)PE=﹣
(x﹣1)2﹣2;(2)PE=﹣![]() x2+
x2+![]() x;(3)P点坐标为(
x;(3)P点坐标为(![]() ﹣1,
﹣1,![]() )或(1+
)或(1+![]() ,
,![]() ﹣1).
﹣1).
【解析】
(1)利用待定系数法求二次函数解析式.(2)先求出直线AB方程,再求出PE长.(3)利用相似的性质,列比例式,再代入,解方程,可求出P点坐标.
(1)设二次函数的解析式为y=a(x﹣1)2﹣2,
∵A(3,0)在抛物线上,
∴0=a(3﹣1)2﹣2
∴a=![]() ,
,
∴y=![]() (x﹣1)2﹣2,
(x﹣1)2﹣2,
(2)抛物线与y轴交点B的坐标为(0,![]() ),
),
设直线AB的解析式为y=kx+m,
∴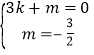 ,
,
∴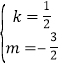 ,
,
∴直线AB的解析式为y=![]() .
.
∵P为线段AB上的一个动点,
∴P点坐标为(x,![]() x﹣
x﹣![]() .).(0<x<3)
.).(0<x<3)
由题意可知PE∥y轴,∴E点坐标为(x,![]() x2﹣x﹣
x2﹣x﹣![]() ),
),
∵0<x<3,
∴PE=(![]() .)﹣(
.)﹣(![]() x2﹣x﹣
x2﹣x﹣![]() )=﹣
)=﹣![]() x2+
x2+![]() .
.
(3)由题意可知D点横坐标为x=1,又D点在直线AB上,
∴D点坐标(1,﹣1).
当∠EDP=90°时,△AOB∽△EDP,
∴![]() .
.
过点D作DQ⊥PE于Q,
∴xQ=xP=x,yQ=﹣1,
∴△DQP∽△AOB∽△EDP,
∴![]() ,
,
又OA=3,OB=![]() ,AB=
,AB=![]() ,
,
又DQ=x﹣1,
∴DP=![]() (x﹣1),
(x﹣1),
∴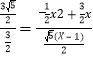 ,
,
解得:x=﹣1±![]() (负值舍去).
(负值舍去).
∴P(![]() ﹣1,
﹣1,![]() )(如图中的P1点);
)(如图中的P1点);
②当∠DEP=90°时,△AOB∽△DEP,
∴![]() .
.
由(2)PE=﹣![]() x2+
x2+![]() .,DE=x﹣1,
.,DE=x﹣1,
∴![]()
解得:x=1±![]() ,(负值舍去).
,(负值舍去).
∴P(1+![]() ,
,![]() ﹣1)(如图中的P2点);
﹣1)(如图中的P2点);
综上所述,P点坐标为(![]() ﹣1,
﹣1,![]() )或(1+
)或(1+![]() ,
,![]() ﹣1).
﹣1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B,C向经过点A的直线EF作垂线,垂足为E,F.

(1)如图1,当EF与斜边BC不相交时,请证明EF=BE+CF;
(2)如图2,当EF与斜边BC相交时,其他条件不变,写出EF、BE、CF之间的数量关系,并说明理由;
(3)如图3,猜想EF、BE、CF之间又存在怎样的数量关系,写出猜想,不必说明理由.
-
科目: 来源: 题型:
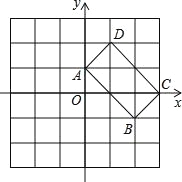
查看答案和解析>>【题目】如图,在 6×6 的网格中,四边形 ABCD 的顶点都在格点上,每个格子都是边长为 1 的正方形,建立如图所示的平面直角坐标系.
(1)画出四边形 ABCD 关于 y 轴对称和四边形 A′B′C′D′(点 A、B、C、D的对称点分别是点 A′B′C′D′.
(2)求 A、B′、B、C 四点组成和四边形的面积.
-
科目: 来源: 题型:
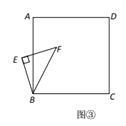
查看答案和解析>>【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)求证:EG=CG且EG⊥CG;
(2)将图①中△BEF绕B点逆时针旋转45,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
 中,
中, 于点
于点 ,
, 于点
于点 ,
, 平分
平分 ,且点
,且点 为
为 的中点,连接
的中点,连接 .
.
(1)求证:
 平分
平分 ;
;(2)求
 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要测量河流
 的长,因为无法测河流附近的点
的长,因为无法测河流附近的点 ,可以在
,可以在 线外任取一点
线外任取一点 ,在
,在 的延长线上任取一点
的延长线上任取一点 ,连结
,连结 和
和 ,并且延长
,并且延长 到点
到点 ,使
,使 ;延长
;延长 到点
到点 ,使
,使 连结
连结 ,并延长
,并延长 到点
到点 ,使点
,使点 ,
, ,
, 在同一直线上.证明:测量出线段
在同一直线上.证明:测量出线段 的长就是河流
的长就是河流 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为10cm,点E在边AB上,且AE=4cm,

(1)如果点P在线段BC上以2cm/s的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
①若点Q的运动速度与点P的运动速度相等,经过2秒后,△BPE与△CQP是否全等?请说明理由.
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为________cm/s时,在某一时刻也能够使△BPE与△CQP全等.
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿正方形ABCD的四条边运动.求经过多少秒后,点P与点Q第一次相遇,并写出第一次相遇点在何处?
相关试题

