【题目】如图,在菱形ABCD中,AB=2,∠BAD=60°,E是边AD的中点,M是边AB上任一点(不与点A重合),延长ME交CD的延长线与点N,连接MD,AN. 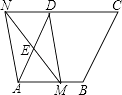
(1)求证:四边形AMDN是平行四边形;
(2)当AM=时,四边形AMDN是矩形(直接写答案即可)
参考答案:
【答案】
(1)证明:∵四边形ABCD是菱形,
∴ND∥AM,
∴∠NDE=∠MAE,∠DNE=∠AME.
∵E是AD中点,
∴DE=AE,
在△NDE和△MAE中, 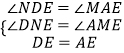 ,
,
∴△NDE≌△MAE(AAS),
∴△NDE≌△MAE,
∴ND=AM,
∴四边形AMDN是平行四边形
(2)1
【解析】(2)解:当AM=1时,四边形AMDN是矩形.理由如下: ∵四边形AMDN是菱形,
∴AD=AB=2,
∵平行四边形AMDN是矩形,
∴DM⊥AB,
即∠AMD=90°.
∵∠BAD=60°,
∴∠ADM=30°,
∴AM= ![]() AD=1;
AD=1;
所以答案是:1.
【考点精析】本题主要考查了平行四边形的判定与性质和菱形的性质的相关知识点,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学进行跳高测试,每人10次跳高的平均成绩恰好是1.6米,方差分别是S甲2=1.2,S乙2=0.5,则在本次测试中,同学的成绩更稳定(填“甲”或“乙”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年遵义市固定资产总投资计划为2580亿元,将2580亿元用科学记数法表示为( )
A.2.58×1011
B.2.58×1012
C.2.58×1013
D.2.58×1014 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.
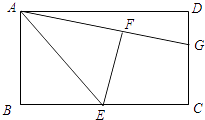
(1)猜想线段GF与GC有何数量关系?并证明你的结论;
(2)若AB=3,AD=4,求线段GC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:四边形ABCD是正方形,E是AB边上一点,F是BC延长线上一点,且DE=DF.
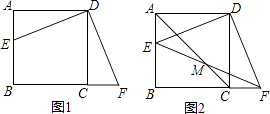
(1)如图1,求证:DF⊥DE;
(2)如图2,连接AC,EF交于点M,求证:M是EF的中点. -
科目: 来源: 题型:
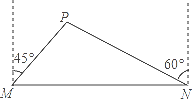
查看答案和解析>>【题目】我市准备在相距2千米的M,N两工厂间修一条笔直的公路,但在M地北偏东45°方向、N地北偏西60°方向的P处,有一个半径为0.6千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:
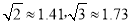 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x﹣1=x2﹣1的根是_____.
相关试题

