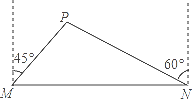
【题目】我市准备在相距2千米的M,N两工厂间修一条笔直的公路,但在M地北偏东45°方向、N地北偏西60°方向的P处,有一个半径为0.6千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据: ![]() )
)
参考答案:
【答案】修的公路不会穿越住宅小区,故该小区居民不需搬迁。
【解析】试题分析:根据题意,在△MNP中,∠MNP=30°,∠PMN=45°,MN=2千米,是否搬迁看P点到MN的距离与0.6的大小关系,若距离大于0.6千米则不需搬迁,反之则需搬迁,因此求P点到MN的距离,作PD⊥MN于D点.
试题解析:过点P作PE⊥MN于E.
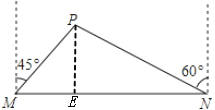
由题意得:∠PNE=90°-60°=30°,∠PME=90°-45°=45°,
∴在Rt△PME中,PE=ME.
∵在Rt△PEN中,∠PNE=30°,
∴EN=![]() =
=![]() PE.
PE.
∵MN=ME+EN=2千米,
∴PE+![]() PE=2,
PE=2,
解得:PE=3√-1≈0.73(千米)>0.6千米.
∴修的公路不会穿越小区,
故该小区居民不需搬迁.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.
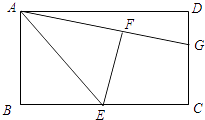
(1)猜想线段GF与GC有何数量关系?并证明你的结论;
(2)若AB=3,AD=4,求线段GC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠BAD=60°,E是边AD的中点,M是边AB上任一点(不与点A重合),延长ME交CD的延长线与点N,连接MD,AN.
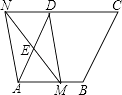
(1)求证:四边形AMDN是平行四边形;
(2)当AM=时,四边形AMDN是矩形(直接写答案即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:四边形ABCD是正方形,E是AB边上一点,F是BC延长线上一点,且DE=DF.
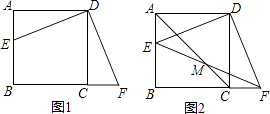
(1)如图1,求证:DF⊥DE;
(2)如图2,连接AC,EF交于点M,求证:M是EF的中点. -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x﹣1=x2﹣1的根是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式﹣6y4+5xy3﹣4x2+x3y是按( )
A.x的降幂排列
B.x的升幂排列
C.y的降幂排列
D.y的升幂排列 -
科目: 来源: 题型:
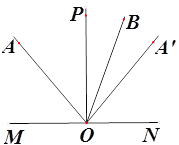
查看答案和解析>>【题目】如图,平面内一定点A在直线MN的上方,点O为直线MN上一动点 ,作射线OA、OP、OA’,当点O在直线MN上运动时,始终保持∠MOP=90°、∠AOP=∠A’OP,将射线OA绕点O顺时针旋转60°得到射线OB
(1)如图,当点O运动到使点A在射线OP的左侧,若OB平分∠A’OP,求∠AOP的度数;
(2)当点O运动到使点A在射线OP的左侧,∠AOM=3∠A’OB时,求
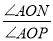 的值;
的值;(3)当点O运动到某一时刻时,∠A’OB=150°,直接写出∠BOP= 度.
相关试题

