【题目】已知:四边形ABCD是正方形,E是AB边上一点,F是BC延长线上一点,且DE=DF. 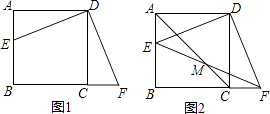
(1)如图1,求证:DF⊥DE;
(2)如图2,连接AC,EF交于点M,求证:M是EF的中点.
参考答案:
【答案】
(1)证明:∵四边形ABCD是正方形,
∴DA=DC,∠DAE=∠DCB=90°.
∴∠DCF=180°﹣90°=90°.
∴∠DAE=∠DCF.
在Rt△DAE和Rt△DCF中, ![]() ,
,
∴Rt△DAE≌Rt△DCF(HL).
∴∠ADE=∠CDF,
∵∠ADE+∠CDE=90°,
∴∠CDF+∠CDE=90°,
即∠EDF=90°,
∴DF⊥DE
(2)证明;过点F作GF⊥CF交AC的延长线于点G,
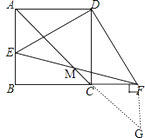
则∠GFC=90°.
∵正方形ABCD中,∠B=90°,
∴∠GFC=∠B.
∴AB∥GF.
∴∠BAC=∠G.
∵四边形ABCD是正方形,
∴AB=BC,
∴∠BAC=∠BCA=45°.
∴∠BAC=∠BCA=∠FCG=∠G=45°.
∴FC=FG.
∵△DAE≌△DCF,
∴AE=CF.
∴AE=FG.
在△AEM和△GFM中, 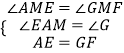 ,
,
∴△AEM≌△GFM(AAS).
∴ME=MF.
即M是EF的中点
【解析】(1)由正方形的性质得出DA=DC,∠DAE=∠DCB=90°.得出∠DAE=∠DCF.由HL证明Rt△DAE≌Rt△DCF,得出∠ADE=∠CDF,证出∠EDF=90°即可;(2)证明;过点F作GF⊥CF交AC的延长线于点G,则∠GFC=90°.AB∥GF.得出∠BAC=∠G.由正方形的性质证出FC=FG.得出AE=FG.由AAS证明△AEM≌△GFM,得出ME=MF即可.
【考点精析】利用正方形的性质对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年遵义市固定资产总投资计划为2580亿元,将2580亿元用科学记数法表示为( )
A.2.58×1011
B.2.58×1012
C.2.58×1013
D.2.58×1014 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.
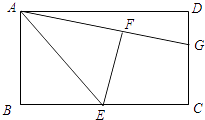
(1)猜想线段GF与GC有何数量关系?并证明你的结论;
(2)若AB=3,AD=4,求线段GC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠BAD=60°,E是边AD的中点,M是边AB上任一点(不与点A重合),延长ME交CD的延长线与点N,连接MD,AN.
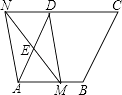
(1)求证:四边形AMDN是平行四边形;
(2)当AM=时,四边形AMDN是矩形(直接写答案即可) -
科目: 来源: 题型:
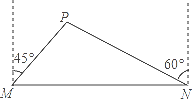
查看答案和解析>>【题目】我市准备在相距2千米的M,N两工厂间修一条笔直的公路,但在M地北偏东45°方向、N地北偏西60°方向的P处,有一个半径为0.6千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:
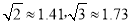 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x﹣1=x2﹣1的根是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式﹣6y4+5xy3﹣4x2+x3y是按( )
A.x的降幂排列
B.x的升幂排列
C.y的降幂排列
D.y的升幂排列
相关试题

