【题目】如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连接CD,过点B作BG丄CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连接DF.给出以下四个结论:
①![]() ; ②点F是GE的中点; ③AF=
; ②点F是GE的中点; ③AF=![]() AB;④S△ABC=5S△BDF,其中正确的结论序号是__________.
AB;④S△ABC=5S△BDF,其中正确的结论序号是__________.

参考答案:
【答案】①③
【解析】试题分析:∵在Rt△ABC中,∠ABC=90°,∴AB⊥BC,AG⊥AB,∴AG∥BC,∴△AFG∽△CFB,
∴![]() ,∵BA=BC,∴
,∵BA=BC,∴![]() ,故①正确;∵∠ABC=90°,BG⊥CD∴∠DBE+∠BDE=∠BDE+∠BCD=90°,
,故①正确;∵∠ABC=90°,BG⊥CD∴∠DBE+∠BDE=∠BDE+∠BCD=90°,
∴∠DBE=∠BCD,∵AB=CB,点D是AB的中点,∴BD=![]() AB=
AB=![]() CB,∵tan∠BCD=
CB,∵tan∠BCD=![]() =
=![]() ,∴在Rt△ABG中,tan∠DBE=
,∴在Rt△ABG中,tan∠DBE=![]() =
=![]() ,∵
,∵![]() ,∴FG=
,∴FG=![]() FB,故②错误;∵△AFG∽△CFB,∴AF:CF=AG:BC=1:2,
FB,故②错误;∵△AFG∽△CFB,∴AF:CF=AG:BC=1:2,
∴AF=![]() AC,∵AC=
AC,∵AC=![]() AB,∴AF=
AB,∴AF=![]() AB,故③正确;∵BD=
AB,故③正确;∵BD=![]() AB,AF=
AB,AF=![]() AC,∴S△ABC=6S△BDF,故④错误.故答案为:①③.
AC,∴S△ABC=6S△BDF,故④错误.故答案为:①③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一次函数y=x+6,下列结论错误的是( )
A. 函数值随自变量增大而增大 B. 函数图像与
 轴正方向成45°角
轴正方向成45°角C. 函数图像不经过第四象限 D. 函数图像与
 轴交点坐标是(0,6)
轴交点坐标是(0,6) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a﹣b+c>0;②3a+b=0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.其中正确结论是( )

A. ①②③ B. ①③④ C. ③④⑤ D. ②③⑤
-
科目: 来源: 题型:
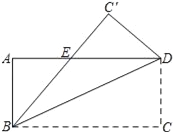
查看答案和解析>>【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若AB=3,AD=9,求△BDE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(2,-4)位于( ).
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=-x+m的图象和y轴交于点B,与正比例函数y=x图象交于点P (2,n).
(1)求m和n的值;
(2)求△POB的面积.
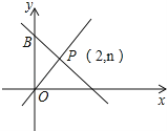
-
科目: 来源: 题型:
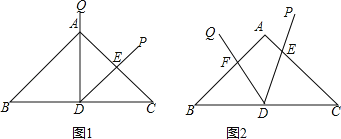
查看答案和解析>>【题目】在等腰△ABC中,AB=AC=10,BC=12,D为底边BC的中点,以D为顶点的角∠PDQ=∠B.
(1)如图1,若射线DQ经过点A,DP交AC边于点E,直接写出与△CDE相似的三角形;
(2)如图2,若射线DQ交AB于点F,DP交AC边于点E,设AF=x,AE为y,试写出y与x的函数关系式;(不要求写出自变量的取值范围)
(3)在(2)的条件下,连接EF,则△DEF与△CDE相似吗?试说明理由.
相关试题

