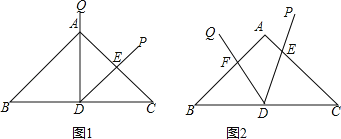
【题目】在等腰△ABC中,AB=AC=10,BC=12,D为底边BC的中点,以D为顶点的角∠PDQ=∠B.
(1)如图1,若射线DQ经过点A,DP交AC边于点E,直接写出与△CDE相似的三角形;
(2)如图2,若射线DQ交AB于点F,DP交AC边于点E,设AF=x,AE为y,试写出y与x的函数关系式;(不要求写出自变量的取值范围)
(3)在(2)的条件下,连接EF,则△DEF与△CDE相似吗?试说明理由.
参考答案:
【答案】(1)(1)与△CDE相似的三角形为△ABD,△ACD,△ADE;理由见解析;(2)y=![]() ;(3)△DEF与△CDE相似.理由见解析.
;(3)△DEF与△CDE相似.理由见解析.
【解析】试题分析:1)由等腰三角形的性质得出∠B=∠C,∠ADB=∠ADC=90°,因此△ABD∽△ACD,证出∠PDQ=∠C,由∠DAE=∠CAD,得出△ADE∽△ACD;在证出△CDE∽△CAD,即可得出结果;
(2)证出△BDF∽△CDE,得出对应边成比例![]() ,即可得出y与x的函数关系式;
,即可得出y与x的函数关系式;
(3)由(2)可知:△BDF∽△CDE,得出![]() 证出
证出![]() ,由∠EDF=∠C,即可得出△DEF∽△CED.
,由∠EDF=∠C,即可得出△DEF∽△CED.
试题分析:(1)与△CDE相似的三角形为△ABD,△ACD,△ADE;理由如下:
∵AB=AC,D为底边BC的中点,
∴∠B=∠C,AD⊥BC,
∴∠ADB=∠ADC=90°,
∴△ABD∽△ACD,
∵∠PDQ=∠B,
∴∠PDQ=∠C,
又∵∠DAE=∠CAD,
∴△ADE∽△ACD;
∵∠CDE+∠PDQ=90°,
∴∠C+∠PDQ=90°,
∴∠CED=90°=∠ADC,
又∵∠C=∠C,
∴△CDE∽△CAD,
∴△△ABD∽△ACD∽△ADE∽△CDE;
(2)∵∠FDC=∠B+∠BDF,
∠FDC=∠FDE+∠EDC,
∴∠EDC=∠BDF,
∴△BDF∽△CDE,
∴![]() ,
,
∵D为BC的中点,
∴BD=CD=6,
∴![]()
∴y=![]() ;
;
(3)△DEF与△CDE相似.理由如下:如图所示:
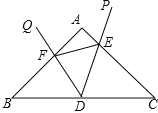
由(2)可知:△BDF∽△CDE,
则![]() ,
,
∵BD=CD,
∴![]() ,
,
又∵∠EDF=∠C,
∴△DEF∽△CED.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连接CD,过点B作BG丄CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连接DF.给出以下四个结论:
①
 ; ②点F是GE的中点; ③AF=
; ②点F是GE的中点; ③AF= AB;④S△ABC=5S△BDF,其中正确的结论序号是__________.
AB;④S△ABC=5S△BDF,其中正确的结论序号是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(2,-4)位于( ).
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=-x+m的图象和y轴交于点B,与正比例函数y=x图象交于点P (2,n).
(1)求m和n的值;
(2)求△POB的面积.
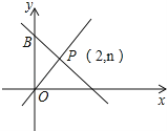
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.3a+4b=12a
B.(ab3)2=ab6
C.(5a2﹣ab)﹣(4a2+2ab)=a2﹣3ab
D.x12÷x6=x2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果仅用一种正多边形进行镶嵌,下列正多边形:正五边形、正方形、正六边形、正八边形、正三角形中不能构成平面镶嵌的有( )个.
A.2
B.3
C.4
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查活动中适合用全面调查的是( )
A.“奔跑吧,兄弟”节目的收视率
B.调查乘坐飞机的旅客是否带了违禁物品
C.某种品牌节能灯的使用寿命
D.了解河北省中学生课外阅读的情况
相关试题

