【题目】如图,已知点A、B、C、D的坐标分别为(-2,2),(一2,1),(3,1),(3,2),线段AD、AB、BC组成的图形记作G,点P沿D-A-B-C移动,设点P移动的距离为a,直线l:y=-x+b过点P,且在点P移动过程中,直线l随点P移动而移动,若直线l过点C,求
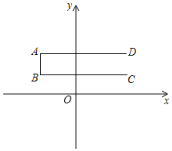
(1)直线l的解析式;
(2)求a的值.
参考答案:
【答案】(1)y=-x+4;(2)当l过点C时,a的值为1或11.
【解析】
(1)将点D坐标代入y=-x+b,解出b,再代回即可得函数的解析式;
(2)l过点C,点P的位置有两种:①点P位于点E时;②点P位于点C时;
(1)当y=-x+b过点C(3,1)时,
1=-3+b,
∴b=4.
直线l的解析式为y=-x+4.
(2)∵点A,B,C,D的坐标分别为(-2,2),(-2,1),(3,1),(3,2).
∴AD=BC=5,AB=1,
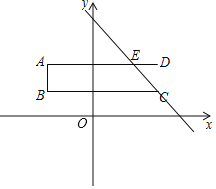
∵直线l的解析式为y=-x+4.
∴由![]() 得l与AD的交点E为(2,2)
得l与AD的交点E为(2,2)
∴DE=1.
∴①当l过点C时,点P位于点E时,a=DE=1;
②当l过点C时,点P位于点C时,a=AD+AB+BC=5+1+5=11.
∴当l过点C时,a的值为1或11.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某港口在某天从0时到12时的水位情况变化曲线.

(1)在这一问题中,自变量是什么?
(2)大约在什么时间水位最深,最深是多少?
(3)大约在什么时间段水位是随着时间推移不断上涨的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某区对即将参加中考的初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
视力
频数(人)
频率
4.0≤x<4.3
20
0.1
4.3≤x<4.6
40
0.2
4.6≤x<4.9
70
0.35
4.9≤x<5.2
a
0.3
5.2≤x<5.5
10
b

(1)本次调查的样本为 ,样本容量为 ;
(2)在频数分布表中,组距为 ,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,计算抽样中视力正常的百分比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个多边形,你能否用一直线去截这个多边形,使得到的新多边形分别满足下列条件:
 画出图形,把截去的部分打上阴影
画出图形,把截去的部分打上阴影
 新多边形内角和比原多边形的内角和增加了
新多边形内角和比原多边形的内角和增加了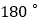 .
. 新多边形的内角和与原多边形的内角和相等.
新多边形的内角和与原多边形的内角和相等. 新多边形的内角和比原多边形的内角和减少了
新多边形的内角和比原多边形的内角和减少了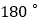 .
. 将多边形只截去一个角,截后形成的多边形的内角和为
将多边形只截去一个角,截后形成的多边形的内角和为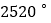 ,求原多边形的边数.
,求原多边形的边数.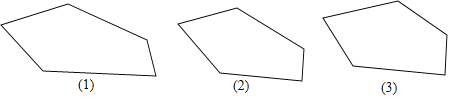
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,点E,F分别在边AB,CD上,点G,H在对角线AC上,EF与AC相交于点O,AG=CH,BE=DF.
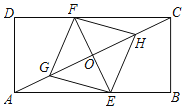
(1)求证:四边形EGFH是平行四边形;
(2)当EG=EH时,连接AF
①求证:AF=FC;
②若DC=8,AD=4,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣,两种型号的机器人的工作效率和价格如表:
型号
甲
乙
每台每小时分拣快递件数(件)
1000
800
每台价格(万元)
5
3
该公司计划购买这两种型号的机器人共10台,并且使这10台机器人每小时分拣快递件数总和不少于8500件
(1)设购买甲种型号的机器人x台,购买这10台机器人所花的费用为y万元,求y与x之间的关系式;
(2)购买几台甲种型号的机器人,能使购买这10台机器人所花总费用最少?最少费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如表(单位:分):
项目人员
阅读能力
思维能力
表达能力
甲
93
86
73
乙
95
81
79
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将能被录用?
(2)根据实际需要,公司将阅读、思维和表达能力三项测试得分按3:5:2的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
(3)公司按照(2)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值,如最右边一组分数x为:85≤x<90),并决定由高分到低分录用8名员工,甲、乙两人能否被录用?请说明理由,并求出本次招聘人才的录用率.
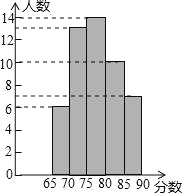
相关试题

