【题目】如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,请探究: 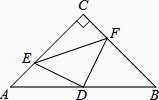
(1)求证:△DFE是等腰直角三角形;
(2)四边形CEDF的面积是否发生变化?若不变化,请求出面积.
参考答案:
【答案】
(1)解:连接CD,
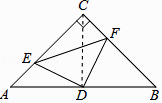
∵△ABC是等腰直角三角形,
∴∠DCB=∠A=45°,CD=AD=DB,
∵AE=CF,
在△ADE与△CDF中,
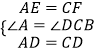 ,
,
∴△ADE≌△CDF,
∴DE=DF,∠CDF=∠ADE,
∵∠ADE+∠CDE=90°,
∴∠CDF+∠CDE=∠EDF=90°,
∴DE⊥DF,
∴△DFE是等腰直角三角形;
(2)解:四边形CEDF的面积不发生变化.
理由:∵△ADE≌△CDF,
∴S△CDF=S△ADE
∴S四边形CEFD=S△ADC.
∴四边形CEDF的面积是为定值,
∴四边形CEDF的面积为 ![]() ×
× ![]() ×4×4=4
×4×4=4
【解析】(1)连接CD,由SAS定理可证△CDF和△ADE全等,从而可证∠EDF=90°,DF=DE.所以△DEF是等腰直角三角形;(2)由割补法可知四边形CDFE的面积保持不变,利用三角形的面积公式求出答案.
【考点精析】本题主要考查了等腰直角三角形的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能正确解答此题.
-
科目: 来源: 题型:
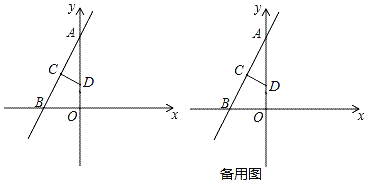
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(0,8),B(﹣4,0),线段AB的垂直平分线CD分别交AB、OA于点C、D,其中点D的坐标为(0,3).
(1)求直线AB的解析式;
(2)求线段CD的长;
(3)点E为y轴上一个动点,当△CDE为等腰三角形时,求E点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据有关资料统计,两个城市之间每天的电话通话次数T与这两个城市的人口数xy(单位:万人)以及两城市间的距离l(单位:km)之间有下列关系式
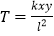 (k为常数) 己知A,B,C三个城市的人口数及它们之间的距离如图所示如果A,B两个城市间每天的电话通话次数为n,求B,C两个城市间每天的电话通话次数(用含n的代数式表示)
(k为常数) 己知A,B,C三个城市的人口数及它们之间的距离如图所示如果A,B两个城市间每天的电话通话次数为n,求B,C两个城市间每天的电话通话次数(用含n的代数式表示)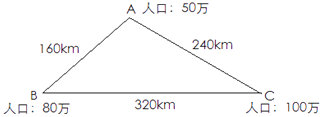
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中.
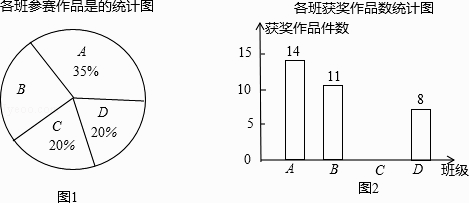
(1)B班参赛作品有多少件?
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高?
(4)将写有A、B、C、D四个字母的完全相同的卡片放入箱中,从中一次随机抽出两张卡片,求抽到A、B两班的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.

(1)求证:直线CD为⊙O的切线;
(2)当AB=2BE,且CE= 时,求AD的长.
时,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
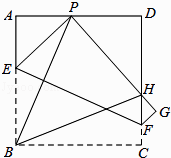
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】小华家买了一辆轿车,他连续10天记录了他家轿车每天行驶的路程,以30千米为标准,超过或不足部分分别用正数、负数表示,得到的数据如下(单位:千米):+3,+1,
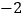 ,+9,
,+9,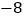 ,+2.5,
,+2.5, ,+4.5,
,+4.5, ,+2
,+2(1)请你运用所学知识估计小华家一个月(按30天算)轿车行驶的路程;
(2)若已知该轿车每行驶100千米耗油8升,目前汽油价格为每升7.8元,试根据(1)题估计小
华家一年(按12个月算)的汽油费用.
相关试题

