【题目】小华家买了一辆轿车,他连续10天记录了他家轿车每天行驶的路程,以30千米为标准,超过或不足部分分别用正数、负数表示,得到的数据如下(单位:千米):+3,+1,![]() ,+9,
,+9,![]() ,+2.5,
,+2.5,![]() ,+4.5,
,+4.5,![]() ,+2
,+2
(1)请你运用所学知识估计小华家一个月(按30天算)轿车行驶的路程;
(2)若已知该轿车每行驶100千米耗油8升,目前汽油价格为每升7.8元,试根据(1)题估计小
华家一年(按12个月算)的汽油费用.
参考答案:
【答案】(1)915km;(2)6851.32元.
【解析】
(1)根据有理数的加法,可得10天的数据和,再根据有理数的乘法,可得答案;
(2)由每天平均的路程,求出一年行驶的路程,除以100得到耗油的升数,乘以每升油的价格即可得到总费用.
解:(1)10×30+(3+1-2+9-8+2.5-4+4.5-3+2)
=300+5
=305(km),
∴30×(305÷10)=915(km).
故小华家的小车一个月(按30天算)行驶的路程是915km;
(2)12×915÷100×8×7.8=6851.52(元),
答:估计小明家的小车一年(按12个月算)的汽油费用是6851.52元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,请探究:
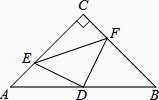
(1)求证:△DFE是等腰直角三角形;
(2)四边形CEDF的面积是否发生变化?若不变化,请求出面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.

(1)求证:直线CD为⊙O的切线;
(2)当AB=2BE,且CE= 时,求AD的长.
时,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
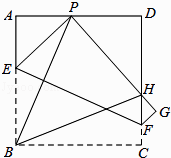
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,已知点
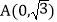 ,
,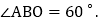 若对于平面内一点C,当
若对于平面内一点C,当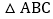 是以AB为腰的等腰三角形时,称点C时线段AB的“等长点”.
是以AB为腰的等腰三角形时,称点C时线段AB的“等长点”.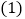 请判断点
请判断点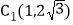 ,点
,点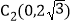 是否是线段AB的“等长点”,并说明理由;
是否是线段AB的“等长点”,并说明理由;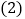 若点
若点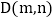 是线段AB的“等长点”,且
是线段AB的“等长点”,且 ,求m和n的值.
,求m和n的值.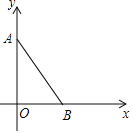
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
①最大的负整数是﹣1;②数轴上表示数2 和﹣2的点到原点的距离相等;③当a≤0时,|a|=﹣a成立;④a的倒数是
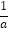 ;⑤(﹣2)2 和﹣22相等.
;⑤(﹣2)2 和﹣22相等.A. 2 个 B. 3 个 C. 4 个 D. 5 个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
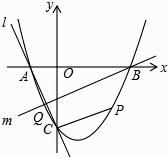
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
相关试题

