【题目】某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中. 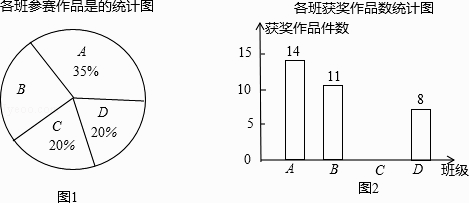
(1)B班参赛作品有多少件?
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高?
(4)将写有A、B、C、D四个字母的完全相同的卡片放入箱中,从中一次随机抽出两张卡片,求抽到A、B两班的概率.
参考答案:
【答案】
(1)解:由题意可得:100×(1﹣35%﹣20%﹣20%)=25(件),
答:B班参赛作品有25件
(2)解:∵C班提供的参赛作品的获奖率为50%,
∴C班的参赛作品的获奖数量为:100×20%×50%=10(件),
如图所示:
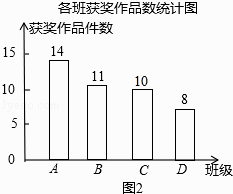 ;
;
(3)解:A班的获奖率为: ![]() ×100%=40%,
×100%=40%,
B班的获奖率为: ![]() ×100%=44%,
×100%=44%,
C班的获奖率为:50%;
D班的获奖率为: ![]() ×100%=40%,
×100%=40%,
故C班的获奖率高
(4)解:如图所示:
![]() ,
,
故一共有12种情况,符合题意的有2种情况,
则从中一次随机抽出两张卡片,求抽到A、B两班的概率为: ![]() =
= ![]()
【解析】(1)直接利用扇形统计图中百分数,进而求出B班参赛作品数量;(2)利用C班提供的参赛作品的获奖率为50%,结合C班参赛数量得出获奖数量;(3)分别求出各班的获奖百分率,进而求出答案;(4)利用树状统计图得出所有符合题意的答案进而求出其概率.
【考点精析】利用扇形统计图和条形统计图对题目进行判断即可得到答案,需要熟知能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F,则下列结论不一定成立的是( )
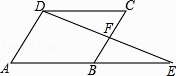
A.∠E=∠CDF
B.EF=DF
C.AD=2BF
D.BE=2CF -
科目: 来源: 题型:
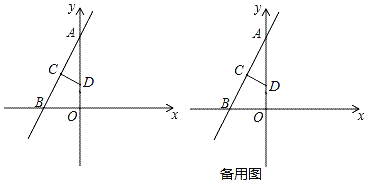
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(0,8),B(﹣4,0),线段AB的垂直平分线CD分别交AB、OA于点C、D,其中点D的坐标为(0,3).
(1)求直线AB的解析式;
(2)求线段CD的长;
(3)点E为y轴上一个动点,当△CDE为等腰三角形时,求E点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据有关资料统计,两个城市之间每天的电话通话次数T与这两个城市的人口数xy(单位:万人)以及两城市间的距离l(单位:km)之间有下列关系式
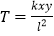 (k为常数) 己知A,B,C三个城市的人口数及它们之间的距离如图所示如果A,B两个城市间每天的电话通话次数为n,求B,C两个城市间每天的电话通话次数(用含n的代数式表示)
(k为常数) 己知A,B,C三个城市的人口数及它们之间的距离如图所示如果A,B两个城市间每天的电话通话次数为n,求B,C两个城市间每天的电话通话次数(用含n的代数式表示)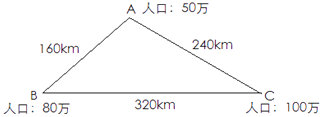
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,请探究:
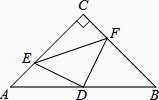
(1)求证:△DFE是等腰直角三角形;
(2)四边形CEDF的面积是否发生变化?若不变化,请求出面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.

(1)求证:直线CD为⊙O的切线;
(2)当AB=2BE,且CE= 时,求AD的长.
时,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
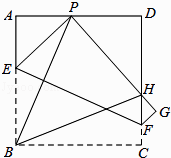
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论.
相关试题

