【题目】如图,一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象交于A(m,3),B(-3,n)两点.
的图象交于A(m,3),B(-3,n)两点.
(1)求一次函数的解析式;
(2)观察函数图象,直接写出关于x的不等式![]() >kx+b的解集.
>kx+b的解集.

参考答案:
【答案】(1) y1=x+1;(2) 0<x<2或x<-3
【解析】试题分析:(1)把A和B代入反比例函数解析式即可求得坐标,然后用待定系数法求得一次函数的解析式;
(2)不等式![]() >kx+b的解集就是:对于相同的x的值,反比例函数的图象在上边的部分自变量的取值范围.
>kx+b的解集就是:对于相同的x的值,反比例函数的图象在上边的部分自变量的取值范围.
试题解析:(1)∵A(m,3),B(-3,n)两点在反比例函数y2=![]() 的图象上,
的图象上,
∴m=2,n=-2.
∴A(2,3),B(-3,-2).
根据题意得: ![]() ,
,
解得: ![]() ,
,
∴一次函数的解析式是:y1=x+1;
(2)根据图象得:0<x<2或x<-3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件中,能判定两个三角形全等的是( )
A. 有三个角对应相等B. 有两条边对应相等
C. 有两边及一角对应相等D. 有两角及一边对应相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到 元购物券,至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
-
科目: 来源: 题型:
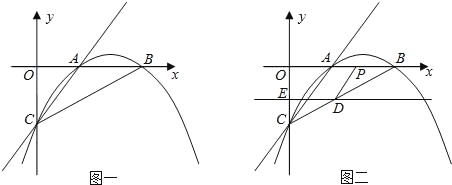
查看答案和解析>>【题目】已知:如图一,抛物线y=ax2+bx+c与x轴正半轴交于A、B两点,与y轴交于点C,直线y=x-2经过A、C两点,且AB=2.
(1)求抛物线的解析式;
(2)若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,(如图2);当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒;设s=
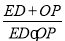 ,当t为何值时,s有最小值,并求出最小值.
,当t为何值时,s有最小值,并求出最小值.(3)在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中正确的是( )
A. a5+a5=2a10 B. a5a5=2a10 C. (﹣4a﹣1)(4a﹣1)=1﹣16a2 D. (a﹣2b)2=a2﹣4b2
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P关于x轴对称点P'的坐标为(4,-5),那么点P关于y轴对称点P''的坐标为( )
A.(4,5)
B.(4,-5)
C.(-4,5)
D.(-4,-5) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),对称轴为x=1,给出四个结论:①b2-4ac>0;②2a+b=0;③a+b=0;④当x=-1或x=3时,函数y的值都等于0,其中正确结论是( )
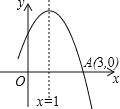
A.②③④ B.①③④ C.①②③ D.①②④
相关试题

