Question

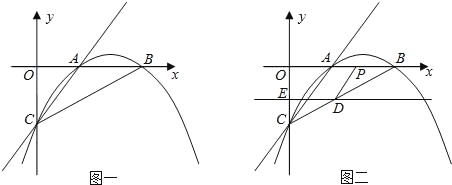
【题目】已知：如图一，抛物线y=ax2+bx+c与x轴正半轴交于A、B两点，与y轴交于点C，直线y=x-2经过A、C两点，且AB=2．

（1）求抛物线的解析式；

（2）若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移，且分别交y轴、线段BC于点E，D，同时动点P从点B出发，沿BO方向以每秒2个单位速度运动，（如图2）；当点P运动到原点O时，直线DE与点P都停止运动，连DP，若点P运动时间为t秒；设s=，当t为何值时，s有最小值，并求出最小值．

（3）在（2）的条件下，是否存在t的值，使以P、B、D为顶点的三角形与△ABC相似；若存在，求t的值；若不存在，请说明理由．

Answer 1

【答案】(1)y=-x2+x-2．（2）当t=1时，s有最小值，且最小值为1．（3）当t=或时，以P、B、D为顶点的三角形与△ABC相似．

【解析】

试题分析：（1）首先根据直线AC的解析式确定点A、C的坐标，已知AB的长，进一步能得到点B的坐标；然后由待定系数法确定抛物线的解析式．

（2）根据所给的s表达式，要解答该题就必须知道ED、OP的长；BP、CE长易知，那么由OP=OB-BP求得OP长，由∠CED的三角函数值可得到ED的长，再代入s的表达式中可得到关于s、t的函数关系式，结合函数的性质即可得到s的最小值．

（3）首先求出BP、BD的长，若以P、B、D为顶点的三角形与△ABC相似，已知的条件是公共角∠OBC，那么必须满足的条件是夹公共角的两组对应边成比例，分两种情况讨论即可．

试题解析：（1）由直线：y=x-2知：A（2，0）、C（0，-2）；

∵AB=2，∴OB=OA+AB=4，即B（4，0）．

设抛物线的解析式为：y=a（x-2）（x-4），代入C（0，-2），得：

a（0-2）（0-4）=-2，解得a=-

∴抛物线的解析式：y=-（x-2）（x-4）=-x2+x-2．

（2）在Rt△OBC中，OB=4，OC=2，则tan∠OCB=2；

∵CE=t，∴DE=2t；

而OP=OB-BP=4-2t；

∴s=（0＜t＜2），

∴当t=1时，s有最小值，且最小值为1．

（3）在Rt△OBC中，OB=4，OC=2，则BC=2；

在Rt△CED中，CE=t，ED=2t，则CD=t；

∴BD=BC-CD=2-t；

以P、B、D为顶点的三角形与△ABC相似，已知∠OBC=∠PBD，则有两种情况：

①，解得t=；

②，解得t=；

综上，当t=或时，以P、B、D为顶点的三角形与△ABC相似．