搜索
【题目】下列条件中，能判定两个三角形全等的是（ ）
A. 有三个角对应相等B. 有两条边对应相等
C. 有两边及一角对应相等D. 有两角及一边对应相等
参考答案：
【答案】D
【解析】
熟练运用判定方法判断．做题时要按判定全等的方法逐个验证．
有三个角对应相等，不能判定全等，A错误；
有两条边对应相等，缺少条件不能判定全等，B错误；
有两边及一角对应相等不能判定全等，C错误；
有两角及一边对应相等可判断全等，符合AAS或ASA，是正确的.
故选D.
-
科目： 来源： 题型：
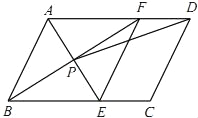
查看答案和解析>>【题目】如图，在ABCD中，AE平分∠BAD，交BC于点E，BF平分∠ABC，交AD于点F，AE与BF交于点P，连接EF，PD．
（1）求证：四边形ABEF是菱形；
（2）若AB=4，AD=6，∠ABC=60°，求tan∠ADP的值．
-
科目： 来源： 题型：
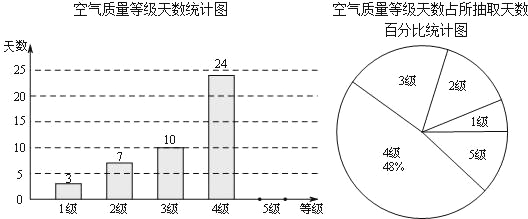
查看答案和解析>>【题目】国家环保局统一规定，空气质量分为5级．当空气污染指数达0-50时为1级，质量为优；51-100时为2级，质量为良；101-200时为3级，轻度污染；201-300时为4级，中度污染；300以上时为5级，重度污染．某城市随机抽取了2015年某些天的空气质量检测结果，并整理绘制成如下两幅不完整的统计图．请根据图中信息，解答下列各题：
（1）本次调查共抽取了 天的空气质量检测结果进行统计；
（2）补全条形统计图；
（3）扇形统计图中3级空气质量所对应的圆心角为 °；
（4）如果空气污染达到中度污染或者以上，将不适宜进行户外活动，根据目前的统计，请你估计2015年该城市有多少天不适宜开展户外活动．
-
科目： 来源： 题型：
查看答案和解析>>【题目】点P（a ， b）关于x轴的对称点为P＇（1，－6），则a ， b的值分别为( )
A.－1，6
B.－1，－6
C.1，－6
D.1，6 -
科目： 来源： 题型：
查看答案和解析>>【题目】某商场为了吸引顾客，设计了一种促销活动：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、“10元”、“20元”和“30元”的字样．规定：顾客在本商场同一日内，每消费满200元，就可以在箱子里先后摸出两个球（第一次摸出后不放回），商场根据两小球所标金额的和返还相应价格的购物券，可以重新在本商场消费，某顾客刚好消费200元．
（1）该顾客至少可得到 元购物券，至多可得到 元购物券；
（2）请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于30元的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图一，抛物线y=ax2+bx+c与x轴正半轴交于A、B两点，与y轴交于点C，直线y=x-2经过A、C两点，且AB=2．
（1）求抛物线的解析式；
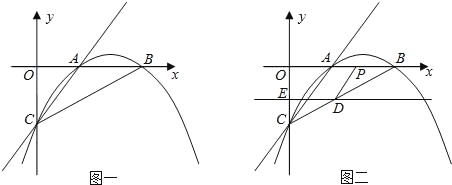
（2）若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移，且分别交y轴、线段BC于点E，D，同时动点P从点B出发，沿BO方向以每秒2个单位速度运动，（如图2）；当点P运动到原点O时，直线DE与点P都停止运动，连DP，若点P运动时间为t秒；设s=
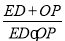，当t为何值时，s有最小值，并求出最小值．（3）在（2）的条件下，是否存在t的值，使以P、B、D为顶点的三角形与△ABC相似；若存在，求t的值；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y1＝kx＋b的图象与反比例函数y2＝
的图象交于A(m，3)，B(－3，n)两点．(1)求一次函数的解析式；
(2)观察函数图象，直接写出关于x的不等式
＞kx＋b的解集．
相关试题
