【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
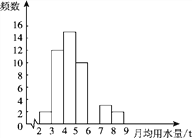
(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
参考答案:
【答案】(1)见解析(2) 279
【解析】试题分析:(1)由已知信息,根据频数、频率和总量的关系,求出月均用水量4≤x<5所占百分比和频数,月均用水量6≤x<7的频数,从而补全频数分布表和频数分布直方图.
(2)求出样本中家庭月均用水量“大于或等于4t且小于7t” 所占百分比,即可用样本估计总体.
试题解析:(1)调查的总数是50户,
则6≤x<7的户数是50×12%=6(户),
则4≤x<5的户数是50-2-12-10-6-3-2=15(户),
所占的百分比是![]() ×100%=30%.
×100%=30%.
补全频数分布表如下:
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | 15 | 30% |
5≤x<6 | 10 | 20% |
6≤x<7 | 6 | 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
补全频数分布直方图如图.
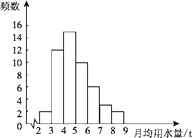
(2)中等用水量家庭大约有450×(30%+20%+12%)=279(户).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=
 ,AF=
,AF=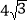 ,求AE的长.
,求AE的长.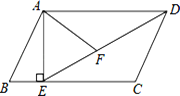
-
科目: 来源: 题型:
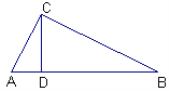
查看答案和解析>>【题目】如图在Rt△ABC中, ∠ACB=90°,CD⊥AB于D.
(1)请直接写出图中所有的相似三角形 (2)你能得出CD2=AD·DB吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12 m,由此他就知道了A,B间的距离,有关他这次探究活动的描述错误的是( )
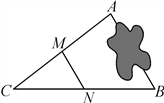
A. AB=24 m B. MN∥AB C. △CMN∽△CAB D. CM∶MA=1∶2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P,且AE=CF.
(1)求证:AF=BE,并求∠FPB的度数;
(2)若AE=2,试求AP·AF的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】4月23日是“世界读书日”,学校开展“让书香溢满校园”读书活动,以提升青少年的阅读兴趣,九年级(1)班数学活动小组对本年级600名学生每天阅读时间进行了统计,根据所得数据绘制了如图所示的两幅不完整的统计图(每组包括最小值不包括最大值)九年级(1)班每天阅读时间在0.5 h以内的学生占全班人数的8%,根据统计图解答下列问题:
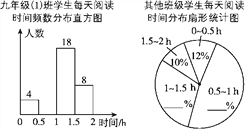
(1)九年级(1)班有________名学生.
(2)补全频数分布直方图.
(3)除九年级(1)班外,九年级其他班级每天阅读时间为1~1.5 h的学生有165人,请你补全扇形统计图.
(4)求该年级每天阅读时间不少于1 h的学生有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC中,D为BC上一点,E为△ABC外部一点,DE交AC于一点O,AC=AE,AD=AB,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)若∠BAD=20°,求∠CDE的度数.

相关试题

