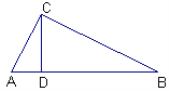
【题目】如图在Rt△ABC中, ∠ACB=90°,CD⊥AB于D.
(1)请直接写出图中所有的相似三角形 (2)你能得出CD2=AD·DB吗?为什么?
参考答案:
【答案】详见解析.
【解析】试题分析:
(1)由已知条件易证:∠ADC=∠BDC=∠ACB=90°,∠B=∠ACD,∠A=∠BCD,因此可得:△ABC∽△ACD, △ABC∽△CBD,△ACD∽△CBD;
(2)由△ACD∽△CBD可得:AD:CD=CD:BD,即CD2=AD![]() BD.
BD.
试题解析:
(1)∵Rt△ABC中, ∠ACB=90°,CD⊥AB于D,
∴∠ADC=∠BDC=∠ACB=90°,
∴∠ACD+∠A=90°,∠A+∠B=90°,∠ACD+∠BCD=90°,
∴∠ACD=∠B,∠A=∠BCD,
∴△ABC∽△ACD, △ABC∽△CBD,△ACD∽△CBD;
(2)能得出CD2=AD·DB,理由如下:
∵△ACD∽△CBD,
∴AD:CD=CD:BD,
∴CD2=AD![]() BD.
BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应南充市创建“全国卫生城市”的号召,某校1 500名学生参加了卫生知识竞赛,成绩记为A、B、C、D四等。从中随机抽取了部分学生成绩进行统计,绘制成如下两幅不完整的统计图表,根据图表信息,以下说法不正确的是( )
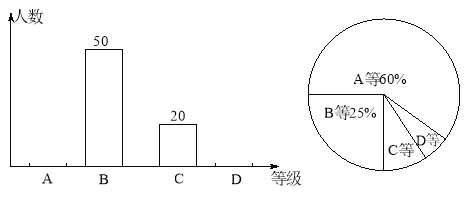
A.样本容量是200
B.D等所在扇形的圆心角为15°
C.样本中C等所占百分比是10%
D.估计全校学生成绩为A等大约有900人
-
科目: 来源: 题型:
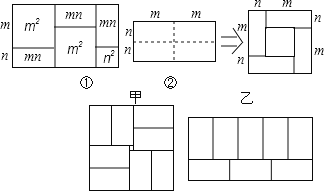
查看答案和解析>>【题目】有许多代数恒等式可以用图形的面积来表示,如图①,它表示了(2m+n)(m+n)=2m2+3mn+n2.
(1)图②是将一个长2m、宽2n的长方形,沿图中虚线平方为四块小长方形,然后再拼成一个正方形,请你观察图形,写出三个代数式(m+n)2、(m-n)2、mn关系的等式: ;
(2)若已知x+y=7、xy=10,则(x-y) 2= ;
(3)小明用8个一样大的长方形(长acm,宽bcm)拼图,拼出了如图甲、乙的两种图案,图案甲是一个正方形,图案乙是一个大的长方形,图案甲的中间留下了边长是2cm的正方形小洞,则(a+2b)2-8ab的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=
 ,AF=
,AF=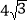 ,求AE的长.
,求AE的长.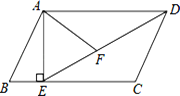
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12 m,由此他就知道了A,B间的距离,有关他这次探究活动的描述错误的是( )
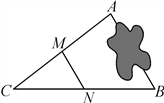
A. AB=24 m B. MN∥AB C. △CMN∽△CAB D. CM∶MA=1∶2
-
科目: 来源: 题型:
查看答案和解析>>【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5
5≤x<6
10
20%
6≤x<7
12%
7≤x<8
3
6%
8≤x<9
2
4%
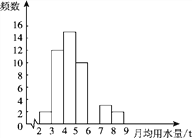
(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P,且AE=CF.
(1)求证:AF=BE,并求∠FPB的度数;
(2)若AE=2,试求AP·AF的值.

相关试题

