【题目】4月23日是“世界读书日”,学校开展“让书香溢满校园”读书活动,以提升青少年的阅读兴趣,九年级(1)班数学活动小组对本年级600名学生每天阅读时间进行了统计,根据所得数据绘制了如图所示的两幅不完整的统计图(每组包括最小值不包括最大值)九年级(1)班每天阅读时间在0.5 h以内的学生占全班人数的8%,根据统计图解答下列问题: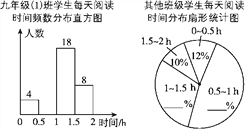
(1)九年级(1)班有________名学生.
(2)补全频数分布直方图.
(3)除九年级(1)班外,九年级其他班级每天阅读时间为1~1.5 h的学生有165人,请你补全扇形统计图.
(4)求该年级每天阅读时间不少于1 h的学生有多少人.
参考答案:
【答案】(1)50(2)见解析(3)见解析(4)246
【解析】试题分析:(1)根据统计图可知0~0.5小时的人数和百分比,用除法可求解;
(2)根据总人数和已知各时间段的人数,求出九年级(1)班学生每天阅读时间在0.5~1 h的人数,画图即可;
(3)根据除九年级(1)班外,九年级其他班级每天阅读时间为1~1.5 h的学生有165人,除以总人数得到百分比,即可画扇形图;
(4)根据扇形统计图求出其它班符合条件的人数,再加上九年级(1)班符合条件的人数即可.
试题解析:(1)4÷8%=50
(2)九年级(1)班学生每天阅读时间在0.5~1 h的有
50-4-18-8=20(人),
补全频数分布直方图如图所示.

(3)因为除九年级(1)班外,九年级其他班级每天阅读时间在1~1.5 h的学生有165人,
所以1~1.5 h在扇形统计图中所占的百分比为165÷(600-50)×100%=30%,
故0.5~1 h在扇形统计图中所占的百分比为1-30%-10%-12%=48%,
补全扇形统计图如图所示.
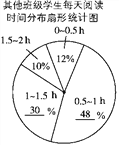
(4)该年级每天阅读时间不少于1 h的学生有(600-50)×(30%+10%)+18+8=246(人).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12 m,由此他就知道了A,B间的距离,有关他这次探究活动的描述错误的是( )
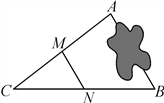
A. AB=24 m B. MN∥AB C. △CMN∽△CAB D. CM∶MA=1∶2
-
科目: 来源: 题型:
查看答案和解析>>【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5
5≤x<6
10
20%
6≤x<7
12%
7≤x<8
3
6%
8≤x<9
2
4%
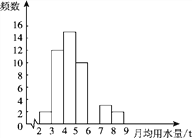
(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P,且AE=CF.
(1)求证:AF=BE,并求∠FPB的度数;
(2)若AE=2,试求AP·AF的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC中,D为BC上一点,E为△ABC外部一点,DE交AC于一点O,AC=AE,AD=AB,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)若∠BAD=20°,求∠CDE的度数.

-
科目: 来源: 题型:
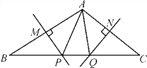
查看答案和解析>>【题目】如图所示,MP和NQ分别垂直平分AB和AC.
(1)若△APQ的周长为12,求BC的长;
(2)∠BAC=105°,求∠PAQ的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)(1)阅读理解:
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是_________;
(2)问题解决:


如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证BE+CF>EF.
相关试题

