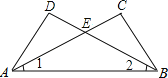
【题目】如图,∠1=∠2,∠C=∠D,AC、BD交于E点,下列结论中不正确的是( )
A.∠DAE=∠CBE
B.△DEA不全等于△CEB
C.CE=DE
D.△EAB是等腰三角形
参考答案:
【答案】B
【解析】
试题分析:根据三角形的内角和定理就可以求出∠DAB=∠CBA,由等式的性质就可以得出∠DAE=∠CBE,根据AAS就可以得出△DEA≌△CEB;由△DEA≌△CEB就可以得出CE=DE,∠1=∠2就可以得出AE=BE,就可以得出结论.
解:∵∠1+∠C+∠ABC=∠2+∠D+∠DAB=180°,且∠1=∠2,∠C=∠D,
∴∠ABC=∠DAB,
∴∠ABC﹣∠2=∠DAB﹣∠1,
∴∠DAB=∠CBA.故A正确;
在△DEA和△CEB中
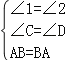 ,
,
∴△DEA≌△CEB(AAS),故B错误;
∴AC=BD.
∵∠1=∠2,
∴BE=AE,
∴△EAB是等腰三角形,AC﹣AE=BD﹣BE,故D正确;
∴CE=DE.故C正确.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2?

-
科目: 来源: 题型:
查看答案和解析>>【题目】小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡行走20m,到达坡顶D处,已知斜坡的坡角为15°.(sin15°=0.259,cos15°=0.966,tan15°=0.268,以下计算结果精确到0.1m)
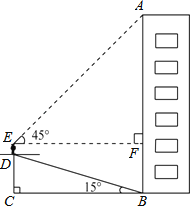
(1)求小华此时与地面的垂直距离CD的值;
(2)小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级教师在讲“解直角三角形”一节时,带领一个小组登上学校教学楼上的一个平台,测量与学校毗邻的一生活小区的一栋居民楼AB的高度,平台C距离地面D高10米,在C处测得居民楼楼底B的俯角为22.5°,楼顶端A的仰角为60°,测完后,记录好数据,回到教师,将示意图画在黑板上,如图所示,要求全班学生按示意图,求出居民楼AB的高度.(最后结果精确到0.1)(参考数据:tan22.5°=
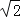 ﹣1,
﹣1,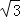 =1.73,
=1.73,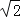 =1.41)
=1.41)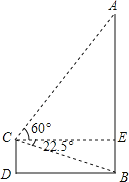
-
科目: 来源: 题型:
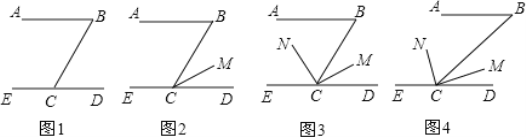
查看答案和解析>>【题目】 (1)①如图1,已知AB∥CD,∠ABC=60°,可得∠BCD=_______°;
②如图2,在①的条件下,如果CM平分∠BCD,则∠BCM=_________°;
③如图3,在①、②的条件下,如果CN⊥CM,则∠BCN=___________°.
(2)、尝试解决下面问题:已知如图4,AB∥CD,∠B=40°,CN是∠BCE的平分线, CN⊥CM,求∠BCM的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c是三角形的三边长,化简:|a﹣b+c|+|a﹣b﹣c|= .
-
科目: 来源: 题型:
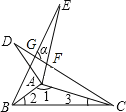
查看答案和解析>>【题目】如图,△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的,若∠1:∠2:∠3=28:5:3,则∠α的度数为 度.
相关试题

