【题目】若函数y=ax2﹣x+a﹣2的图象经过(1,3),则a=_____.
参考答案:
【答案】3.
【解析】
利用待定系数法即可解决问题.
∵函数y=ax2﹣x+a﹣2的图象经过(1,3),
∴3=a﹣1+a﹣2,
∴a=3,
故答案为:3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2+2x+1=0的根的情况是( )
A. 有两个相等的实数根 B. 有两个不相等的实数根
C. 没有实数根 D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的是( )
A.形状相同的两个三角形是全等形
B.面积相等的两个三角形全等
C.周长相等的两个三角形全等
D.周长相等的两个等边三角形全等 -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂有20名工人,每人每天加工甲种零件5个或乙种零件4个.在这20名工人当中,派x人加工甲种零件,其余的加工乙种零件,已知每加工一个甲种零件可获利16元,每加工一个乙种零件可以获利24元.
(1)写出此工厂每天所获利润y(元)与x(人)之间的函数关系式(只写出解析式)
(2)若要使工厂每天获利不低于1800元,问至少要派多少人加工乙种零件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC中,AB=AC,∠BAC=120°,D为BC上一点,AD=DC=2,
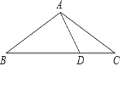
(1)求AC的长;
(2)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正多边形的一个外角为36°,则这个正多边形的边数是( )
A.8
B.9
C.10
D.11 -
科目: 来源: 题型:
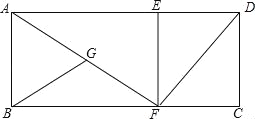
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=25,AB=12,点E、F分别是AD、BC上的点,且DE=CF=9,连接EF、DF、AF.取AF的中点为G,连接BG,将△BFG沿BC方向平移,当点F到达点C时停止平移,然后将△GFB绕C点顺时针旋转α(0°<α<90°),得到△B1CG1(点G的对应点为G1,点B的对应点为B1),在旋转过程中,直线B1G1与直线EF、FD分别相交M、N,当△FMN是等腰三角形,且FM=FN时,线段DN的长为 .
相关试题

