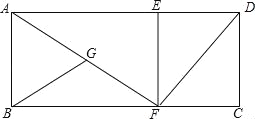
【题目】如图,在矩形ABCD中,AD=25,AB=12,点E、F分别是AD、BC上的点,且DE=CF=9,连接EF、DF、AF.取AF的中点为G,连接BG,将△BFG沿BC方向平移,当点F到达点C时停止平移,然后将△GFB绕C点顺时针旋转α(0°<α<90°),得到△B1CG1(点G的对应点为G1,点B的对应点为B1),在旋转过程中,直线B1G1与直线EF、FD分别相交M、N,当△FMN是等腰三角形,且FM=FN时,线段DN的长为 .
参考答案:
【答案】![]() .
.
【解析】
试题解析:如图,作FL⊥BG于L,FH⊥MN于H,CK⊥MN于K,CR⊥FH于R.FH交ED于T,作TQ⊥DF于Q.
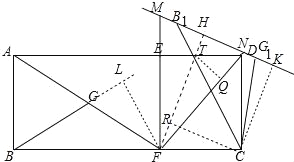
∵四边形ABCD是矩形,
∴∠ABC=∠ADC=∠BCD=90°,AB=CD=12,AD=CF=25,
∵DE=CF=9,又∵DE∥CF,
∴四边形DEFC是平行四边形,
∵∠EDC=90°,
∴四边形DEFC是矩形,同理四边形AEFB是矩形,
∴DF=![]() =15,AF=
=15,AF=![]() =20,
=20,
∵AG=GF,
∴S△BGF=![]() S△ABF=96=
S△ABF=96=![]() BGLF,
BGLF,
∴FL=![]() ,
,
∵CK=FL,
∴CK=![]() ,
,
∵FM=FN,FH⊥MN,CK⊥MN,CR⊥FH,
∴∠RHK=∠HKC=∠KCR=90°,
∴四边形RHKC是矩形,
∴RH=CK=![]() ,
,
∴∠MFH=∠NFH,
∴TE=TQ,设TE=TQ=x,
在RT△TQD中,∵TQ2+QD2=TD2,
∴x2+32=(9-x)2,
∴x=4,
∴FT=![]() ,
,
∵∠EFT+∠CFR=90°,∠CFR+∠FCR=90°,
∴∠EFT=∠FCR,∵∠FET=∠CFR=90°,
∴△FET∽△CFR,
∴![]() ,
,
∴![]() ,
,
∴RF=![]() ,
,
∴FH=FR+RH=![]() ,
,
∵∠HFN=∠HFM,
∴cos∠HFN=![]() ,
,
∴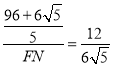 ,
,
∴FN=![]() 3,
3,
∴DN=FN-DF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y=ax2﹣x+a﹣2的图象经过(1,3),则a=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC中,AB=AC,∠BAC=120°,D为BC上一点,AD=DC=2,
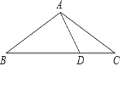
(1)求AC的长;
(2)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正多边形的一个外角为36°,则这个正多边形的边数是( )
A.8
B.9
C.10
D.11 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣x+5的图象与反比例函数
 (k≠0)在第一象限的图象交于A(1,n)和B两点.
(k≠0)在第一象限的图象交于A(1,n)和B两点.
(1)求反比例函数的解析式及点B坐标;
(2)在第一象限内,当一次函数y=-x+5的值大于反比例函数
 (k≠0)的值时,写出自变量x的取值范围.
(k≠0)的值时,写出自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两边长是3和6,则等腰三角形的周长为( )
A.12B.12或15C.15D.14
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年3月,我校举办了以“读城记”为主题的校读书节暨文化艺术节,为了解初中学生更喜欢下列A、B、C、D哪个比赛,从初中学生随机抽取了部分学生进行调查,每个参与调查的学生只选择最喜欢的一个项目,并把调查结果绘制了两幅不完整的统计图,请回答下列问题:
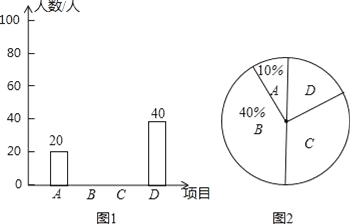
A.“寻找星主播”校园主持人大赛
B.“育才音超”校园歌手大赛
C.阅读之星评选
D.“超级演说家”演讲比赛
(1)这次被调查的学生共有 人.请你将统计图补充完整.
(2)在此调查汇总,抽到了七年级(1)班3人.其中2人喜欢“育才音超”校园歌手大赛、1人喜欢阅读之星评选.抽到八年级(5)班2人,其中1人喜欢“超级演说家”演讲比赛、1人喜欢阅读之星评选.从这5人中随机选两人.用列表或用树状图求出两人都喜欢阅读之星评选的概率.
相关试题

