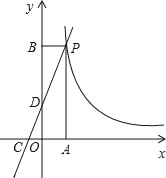
【题目】如图,一次函数y=kx+2的图象与反比例函数y=![]() 的图象在第一象限的交点于P,函数y=kx+2的图象分别交x轴、y轴于点C、D,已知△OCD的面积S△OCD=1,OA=2OC
的图象在第一象限的交点于P,函数y=kx+2的图象分别交x轴、y轴于点C、D,已知△OCD的面积S△OCD=1,OA=2OC
(1)点D的坐标为 ;
(2)求一次函数解析式及m的值;
(3)写出当x>0时,不等式kx+2>![]() 的解集.
的解集.
参考答案:
【答案】(1)(0,2)(2)12(3)x>2
【解析】
(1)利用y轴上的点的坐标特征,利用解析式y=kx+2确定D点坐标;
(2)利用S△OCD=1求出OC的长得到C点坐标,则把C点坐标代入y=kx+2求出k得到一次函数解析式;再利用一次函数解析式求出P点坐标,然后利用反比例函数图象上点的坐标特征求出m的值;
(3)在第一象限内,写出一次函数图象再反比例函数图象上方所对应的自变量的范围即可.
解:(1)当x=0时,y=kx+2=2,则D(0,2),
故答案为(0,2);
(2)∵S△OCD=1,
∴![]() ODOC=1,
ODOC=1,
∴OC=1,
∴C(﹣1,0),
把C(﹣1,0)代入y=kx+2得﹣k+2=0,解得k=2,
∴一次函数解析式为y=2x+2;
∵OA=2OC=2,
∴P点的横坐标为2,
当x=2时,y=2x+2=6,
∴P(2,6),
把P(2,6)代入y=![]() ,
,
∴m=2×6=12;
(3)不等式kx+2>![]() 的解集为x>2.
的解集为x>2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(0,0),B(2,0),点C在y轴上,且S△ABC=3.
(1)求点C的坐标;
(2)以点A、B、C为顶点,作长方形,试写出该长方形第四个顶点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,BA⊥y轴于点A,BC⊥x轴于点C,函数y=﹣
 (x>0)的图象分别交BA、BC于点D、E,当BD=3AD,且△BDE的面积为18时,则k的值是_____.
(x>0)的图象分别交BA、BC于点D、E,当BD=3AD,且△BDE的面积为18时,则k的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为保护学生的身体健康,某中学课桌椅的高度都是按一定的关系配套设计的,下表列出5套符合条件的课桌椅的高度.
椅子高度x(cm)
45
42
39
36
33
桌子高度y(cm)
84
79
74
69
64
(1)假设课桌的高度为ycm,椅子的高度为xcm,请确定y与x的函数关系式;
(2)现有一把高38cm的椅子和一张高73.5cm的课桌,它们是否配套?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某一路口某一时段的汽车流量,小明同学10天中在同一时段统计通过该路口的汽车数量(单位:辆),将统计结果绘制成如下折线统计图:

由此估计一个月(30天)该时段通过该路口的汽车数量超过200辆的天数为( )
A.9
B.10
C.12
D.15 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题提出:如图已知直线OA的解析式是y=2x,OC⊥OA,求直线OC的函数解析式.
甲同学提出了他的想法:在直线y=2x上取一点M,过M作x轴的垂线,垂足为D设点M的横坐标为m,则点M的纵坐标为2m.即OD=m,MD=2m,然后在OC上截取ON=OM,过N作x轴的垂线垂足为B.则点N的坐标为 ,直线OC的解析式为 .
(2)拓展:已知直线OA的解析式是y=kx,OC⊥OA,求直线OC的函数解析式.
(3)应用:直接写出经过P(2,3),且垂直于直线y=﹣
 x+2的直线解析式 .
x+2的直线解析式 .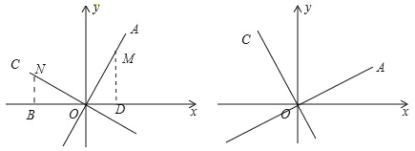
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知射线OM,ON,∠MON=45°点A在射线OM上,点B在射线ON上,OA=1,若△AOB是轴对称图形,点P为AB的中点,则OP2= .
相关试题

