【题目】为保护学生的身体健康,某中学课桌椅的高度都是按一定的关系配套设计的,下表列出5套符合条件的课桌椅的高度.
椅子高度x(cm) | 45 | 42 | 39 | 36 | 33 |
桌子高度y(cm) | 84 | 79 | 74 | 69 | 64 |
(1)假设课桌的高度为ycm,椅子的高度为xcm,请确定y与x的函数关系式;
(2)现有一把高38cm的椅子和一张高73.5cm的课桌,它们是否配套?为什么?
参考答案:
【答案】(1)y=![]() x+3(2)高38cm的椅子和一张高73.5cm的课桌不配套
x+3(2)高38cm的椅子和一张高73.5cm的课桌不配套
【解析】
(1)根据表格中的数据可以设出对应的函数解析式,进而求得函数解析式,从而可以解答本题;
(2)根据(1)中的函数关系式可以解答本题.
(1)假设桌子的高度y与椅子的高度x之间的函数关系式为y=kx+b(k≠0),
![]() ,得
,得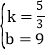 ,
,
∴y=![]() ,
,
当x=39时,y=74,当x=36时,y=69,当x=33时,y=64,
∴y与x的函数关系式为y=![]() ;
;
(2)高38cm的椅子和一张高73.5cm的课桌不配套,
理由:当x=38时,y=![]() =72
=72![]() ≠72.5,
≠72.5,
∴高38cm的椅子和一张高73.5cm的课桌不配套.
-
科目: 来源: 题型:
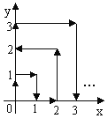
查看答案和解析>>【题目】如图,一个点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点(0,0)运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)…,且每秒移动一个单位,那么第2019秒时这个点所在位置的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(0,0),B(2,0),点C在y轴上,且S△ABC=3.
(1)求点C的坐标;
(2)以点A、B、C为顶点,作长方形,试写出该长方形第四个顶点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,BA⊥y轴于点A,BC⊥x轴于点C,函数y=﹣
 (x>0)的图象分别交BA、BC于点D、E,当BD=3AD,且△BDE的面积为18时,则k的值是_____.
(x>0)的图象分别交BA、BC于点D、E,当BD=3AD,且△BDE的面积为18时,则k的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+2的图象与反比例函数y=
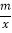 的图象在第一象限的交点于P,函数y=kx+2的图象分别交x轴、y轴于点C、D,已知△OCD的面积S△OCD=1,OA=2OC
的图象在第一象限的交点于P,函数y=kx+2的图象分别交x轴、y轴于点C、D,已知△OCD的面积S△OCD=1,OA=2OC(1)点D的坐标为 ;
(2)求一次函数解析式及m的值;
(3)写出当x>0时,不等式kx+2>
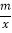 的解集.
的解集.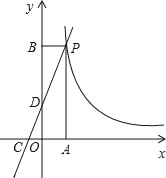
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某一路口某一时段的汽车流量,小明同学10天中在同一时段统计通过该路口的汽车数量(单位:辆),将统计结果绘制成如下折线统计图:

由此估计一个月(30天)该时段通过该路口的汽车数量超过200辆的天数为( )
A.9
B.10
C.12
D.15 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题提出:如图已知直线OA的解析式是y=2x,OC⊥OA,求直线OC的函数解析式.
甲同学提出了他的想法:在直线y=2x上取一点M,过M作x轴的垂线,垂足为D设点M的横坐标为m,则点M的纵坐标为2m.即OD=m,MD=2m,然后在OC上截取ON=OM,过N作x轴的垂线垂足为B.则点N的坐标为 ,直线OC的解析式为 .
(2)拓展:已知直线OA的解析式是y=kx,OC⊥OA,求直线OC的函数解析式.
(3)应用:直接写出经过P(2,3),且垂直于直线y=﹣
 x+2的直线解析式 .
x+2的直线解析式 .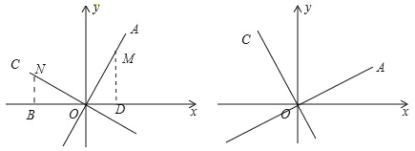
相关试题

