搜索
【题目】为了解某一路口某一时段的汽车流量，小明同学10天中在同一时段统计通过该路口的汽车数量（单位：辆），将统计结果绘制成如下折线统计图：
由此估计一个月（30天）该时段通过该路口的汽车数量超过200辆的天数为（ ）
A.9
B.10
C.12
D.15
参考答案：
【答案】C
【解析】解：由图可知，10天中在同一时段通过该路口的汽车数量超过200辆的有4天，频率为： 
=0.4，
所以估计一个月（30天）该时段通过该路口的汽车数量超过200辆的天数为：30×0.4=12（天）．
故答案为：C．
由图可知，10天中在同一时段通过该路口的汽车数量超过200辆的有4天，从而根据概率公式求出概率，然后利用样本估计总体的方式算出估计一个月（30天）该时段通过该路口的汽车数量超过200辆的天数。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，BA⊥y轴于点A，BC⊥x轴于点C，函数y＝﹣
（x＞0）的图象分别交BA、BC于点D、E，当BD＝3AD，且△BDE的面积为18时，则k的值是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为保护学生的身体健康，某中学课桌椅的高度都是按一定的关系配套设计的，下表列出5套符合条件的课桌椅的高度．
椅子高度x（cm）
45
42
39
36
33
桌子高度y（cm）
84
79
74
69
64
（1）假设课桌的高度为ycm，椅子的高度为xcm，请确定y与x的函数关系式；
（2）现有一把高38cm的椅子和一张高73.5cm的课桌，它们是否配套？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y＝kx+2的图象与反比例函数y＝
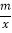的图象在第一象限的交点于P，函数y＝kx+2的图象分别交x轴、y轴于点C、D，已知△OCD的面积S△OCD＝1，OA＝2OC（1）点D的坐标为 ；
（2）求一次函数解析式及m的值；
（3）写出当x＞0时，不等式kx+2＞
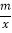的解集．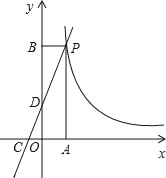
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）问题提出：如图已知直线OA的解析式是y＝2x，OC⊥OA，求直线OC的函数解析式．
甲同学提出了他的想法：在直线y＝2x上取一点M，过M作x轴的垂线，垂足为D设点M的横坐标为m，则点M的纵坐标为2m．即OD＝m，MD＝2m，然后在OC上截取ON＝OM，过N作x轴的垂线垂足为B．则点N的坐标为 ，直线OC的解析式为 ．
（2）拓展：已知直线OA的解析式是y＝kx，OC⊥OA，求直线OC的函数解析式．
（3）应用：直接写出经过P（2，3），且垂直于直线y＝﹣
x+2的直线解析式 ．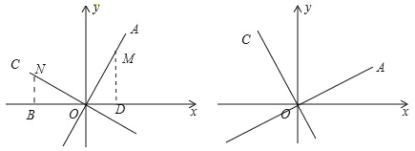
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知射线OM，ON，∠MON=45°点A在射线OM上，点B在射线ON上，OA=1，若△AOB是轴对称图形，点P为AB的中点，则OP2= ．
-
科目： 来源： 题型：
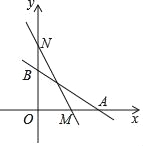
查看答案和解析>>【题目】如图，直线：y＝﹣
x+b与x轴分别交于A（4，0）、B两点，在y轴上有一点N（0，4），动点M从点A以每秒1个单位的速度匀速沿x轴向左移动．（1）点B的坐标为 ；
（2）求△MNO的面积S与移动时间t之间的函数关系式；
（3）当t＝ 时，△NOM≌△AOB；
（4）若M在x轴正半轴上，且△NOM≌△AOB，G是线段ON上一点，连结MG，将△MGN沿MG折叠，点N恰好落在x轴上的H处，求G点的坐标．
相关试题
