【题目】已知∠AOC与∠BOD具有公共顶点,∠COD是两个角叠合的部分.
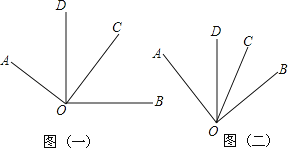
(1)若∠AOC=∠BOD=90°,观察图形(一)并完成下列问题:
①直接写出图中两个相等的锐角: = ;
②如果∠COD=40°,则∠AOB= ,若∠AOB=150°,则∠COD= ;
③猜想∠AOB+∠DOC= °,请说明理由.
(2)探究图形(二):若∠AOC=60°,∠BOD=50°,则∠AOB+∠DOC= °,请说明理由.
参考答案:
【答案】(1)①∠AOD,∠BOC;②140°,30°;③180°,理由见解析;(2)110°,理由见解析
【解析】
(1)①利用同角的余角相等得出答案即可;
②③利用余角的意义和角的和差计算即可;
(2)利用角的和与差计算即可.
解:(1)①若∠AOC=∠BOD=90°,
∠AOD+∠COD=∠BOC+∠COD=90°,
∴∠AOD=∠BOC;
②∵∠COD=40°,
∴∠AOD=50°,
∠AOB=∠AOD+∠BOD=140°;
若∠AOB=150°,则∠AOD=∠AOB﹣90°=60°,
∴∠COD=90°﹣∠AOD=30°.
③∠AOB+∠DOC=180°,
理由:∠AOB+∠DOC=90°+∠AOD+∠DOC=90°+90°=180°;
(2)∠AOB+∠DOC=110°,
理由:若∠AOC=60°,∠BOD=50°,
则∠AOB+∠DOC=∠AOD+∠DOC+∠BOC+∠DOC=∠AOC+∠BOD=110°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条不完整的数轴上从左到右有点A,B,D,C,其中AB=2,BD=3,DC=1,如图所示,设点A,B,D,C所对应数的和是p.

(1)①若以B为原点.写出点A,D,C所对应的数,并计算p的值;
②若以D为原点,p的值是 若以C为原点,p的值是 .
(2)若原点O在图中数轴上点C的右边,且CO=15,p的值是 .
-
科目: 来源: 题型:
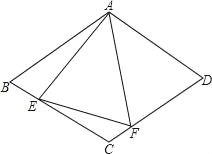
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形的边BC,CD上.
(1)证明:BE=CF.
(2)当点E,F分别在边BC,CD上移动时(△AEF保持为正三角形),请探究四边形AECF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标平面内,直线y=
 x+2分别与x轴、y轴交于点A、C.抛物线y=﹣
x+2分别与x轴、y轴交于点A、C.抛物线y=﹣ +bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.
+bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.(1)求上述抛物线的表达式;
(2)联结BC、BD,且BD交AC于点E,如果△ABE的面积与△ABC的面积之比为4:5,求∠DBA的余切值;
(3)过点D作DF⊥AC,垂足为点F,联结CD.若△CFD与△AOC相似,求点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,⊙P的圆心坐标是(5,a)(a>5),半径为5,函数y=x的图象被⊙P截得的弦AB的长为8,则a的值是( )
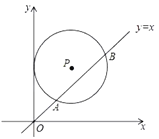
A. 8 B. 5+3
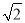 C. 5
C. 5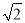 D. 5+
D. 5+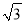
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC是平行四边形,边OC在x轴的负半轴上,反比例函数
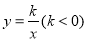 的图象经过点A与BC的中点F,连接AF,OF,若△AOF的面积为12,则k的值为_______.
的图象经过点A与BC的中点F,连接AF,OF,若△AOF的面积为12,则k的值为_______.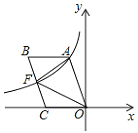
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
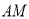 是
是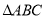 的中线,点
的中线,点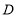 是线段
是线段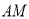 上一点(不与点
上一点(不与点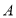 重合).过点
重合).过点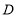 作
作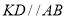 ,交
,交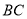 于点
于点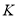 ,过点
,过点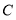 作
作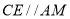 ,交
,交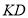 的延长线于点
的延长线于点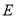 ,连接
,连接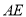 、
、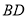 .
.(1)求证:
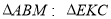 ;
;(2)求证:
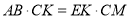 ;
;(3)判断线段
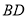 、
、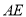 的关系,并说明理由.
的关系,并说明理由.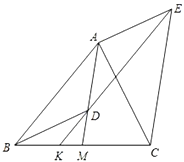
相关试题

