【题目】函数y=kx+k,与y= ![]() 在同一坐标系中的图象大致如图,则( )
在同一坐标系中的图象大致如图,则( )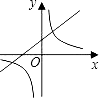
A.K﹥0
B.K﹤0
C.-1﹤K﹤0
D.K﹤-1
参考答案:
【答案】A
【解析】由图可知,函数 ![]() 在第一、二、三象限中,可得k>0,又
在第一、二、三象限中,可得k>0,又 ![]() 反比例函数
反比例函数 ![]() 在第一、三象限中,
在第一、三象限中, ![]() k>0,综上所述,k>0.
k>0,综上所述,k>0.
【考点精析】关于本题考查的一次函数的性质和一次函数的图象和性质,需要了解一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两船从港口A同时出发,甲船以每小时30海里的速度向北偏东35°方向航行,乙船以每小时40海里的速度向另一方向航行,1小时后,甲船到达C岛,乙船达到B岛,若C、B两岛相距50海里,则乙船的航行方向为南偏东多少度?
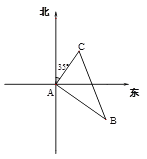
-
科目: 来源: 题型:
查看答案和解析>>【题目】市场上甲种商品的采购价为60元/件,乙种商品的采购价为100元/件,某商店需要采购甲、乙两种商品共15件,且乙种商品的件数不少于甲种商品件数的2倍.设购买甲种商品
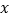 件(
件(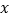 >0),购买两种商品共花费
>0),购买两种商品共花费 元.
元.(1)求出
 与
与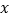 的函数关系式(写出自变量
的函数关系式(写出自变量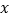 的取值范围);
的取值范围);(2)试利用函数的性质说明,当采购多少件甲种商品时,所需要的费用最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线y=3x+m经过第一、三、四象限,则抛物线y=(x-m)
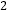 +1的顶点在第象限( )
+1的顶点在第象限( )
A.一
B.二
C.三
D.四 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为线段AD上一点,CO⊥AD于点O,OA=OB,OC=OD,点M、N分别是AC、BD的中点,连接OM、ON、MN.
(1)求证:AC=BD;
(2)试判断△MON的形状,并说明理由;
(3)若AC=2,在图2中,点M在DB的延长线上,求△AMD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A城出发沿一条笔直公路匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离
 (千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.
(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.(1)A,B两城相距 千米,乙车比甲车早到 小时;
(2)甲车出发多长时间与乙车相遇?
(3)若两车相距不超过20千米时可以通过无线电相互通话,则两车都在行驶过程中可以通过无线电通话的时间有多长?

-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=x
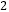 -4x+c的图象与x轴没有交点,其中c为常数,则C的取值范围 是( )
-4x+c的图象与x轴没有交点,其中c为常数,则C的取值范围 是( )
A.c<4
B.c≤4
C.c﹥4
D.c≥4
相关试题

