【题目】市场上甲种商品的采购价为60元/件,乙种商品的采购价为100元/件,某商店需要采购甲、乙两种商品共15件,且乙种商品的件数不少于甲种商品件数的2倍.设购买甲种商品![]() 件(
件(![]() >0),购买两种商品共花费
>0),购买两种商品共花费![]() 元.
元.
(1)求出![]() 与
与![]() 的函数关系式(写出自变量
的函数关系式(写出自变量![]() 的取值范围);
的取值范围);
(2)试利用函数的性质说明,当采购多少件甲种商品时,所需要的费用最少?
参考答案:
【答案】(1)![]() (2)当x=5时,最少费用为1300元
(2)当x=5时,最少费用为1300元
【解析】
根据甲、乙两种商品共15件,购买甲种商品有x件,则乙商品则有(15-x)件,根据乙种商品的件数不少于甲种商品件数的2倍,列出不等式组,求出x的取值范围,再根据甲、乙两种商品的价格列出一次函数关系式即可;
(2)根据(1)得出一次函数y随x的增大而减少,再根据x的取值范围,即可得出当x=5时,所需要的费用最少.
(1)y=60x+100(15-x)=-40x+1500,
∵![]()
∴0![]() x≤5,
x≤5,
即y=-40x+1500(0![]() x≤5);
x≤5);
(2)∵k=-40<0,
∴y随x的增大而减小.即当x取最大值5时,y最小;
此时y=-40×5+1500=1300,
∴当采购5件甲种商品时,所需要的费用最少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)3x3x9﹣2xx3x8
(2)﹣12+20160+(
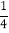 )2017×(﹣4)2018
)2017×(﹣4)2018(3)(x+4)(x﹣4)﹣(x﹣2)2
(4)ab(a+b)﹣(a﹣b)(a2+b2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手.先分别计算下列各式的值.
①(x﹣1)(x+1)=x2﹣1
②(x﹣1)(x2+x+1)=x3﹣1
③(x﹣1)(x3+x2+x+1)=x4﹣1
……
由此我们可以得到:(x﹣1)(x99+x98+x97+…+x+1)=
请你利用上面的结论,再完成下面两题的计算:
(1)(﹣2)50+(﹣2)49+(﹣2)48+…+(﹣2)+1
(2)若x3+x2+x+1=0,求x2019的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两船从港口A同时出发,甲船以每小时30海里的速度向北偏东35°方向航行,乙船以每小时40海里的速度向另一方向航行,1小时后,甲船到达C岛,乙船达到B岛,若C、B两岛相距50海里,则乙船的航行方向为南偏东多少度?
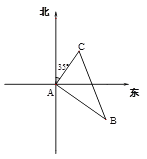
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线y=3x+m经过第一、三、四象限,则抛物线y=(x-m)
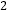 +1的顶点在第象限( )
+1的顶点在第象限( )
A.一
B.二
C.三
D.四 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=kx+k,与y=
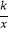 在同一坐标系中的图象大致如图,则( )
在同一坐标系中的图象大致如图,则( )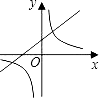
A.K﹥0
B.K﹤0
C.-1﹤K﹤0
D.K﹤-1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为线段AD上一点,CO⊥AD于点O,OA=OB,OC=OD,点M、N分别是AC、BD的中点,连接OM、ON、MN.
(1)求证:AC=BD;
(2)试判断△MON的形状,并说明理由;
(3)若AC=2,在图2中,点M在DB的延长线上,求△AMD的面积.

相关试题

