【题目】甲、乙两车从A城出发沿一条笔直公路匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离![]() (千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.
(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.
(1)A,B两城相距 千米,乙车比甲车早到 小时;
(2)甲车出发多长时间与乙车相遇?
(3)若两车相距不超过20千米时可以通过无线电相互通话,则两车都在行驶过程中可以通过无线电通话的时间有多长?

参考答案:
【答案】(1)300千米,1小时(2)2.5小时(3)1小时
【解析】
(1)根据函数图象可以直接得到A,B两城的距离,乙车将比甲车早到几小时;
(2)由图象所给数据可求得甲、乙两车离开A城的距离y与时间t的关系式,求得两函数图象的交点即可
(3)再令两函数解析式的差小于或等于20,可求得t可得出答案.
(1)由图象可知A、B两城市之间的距离为300km, 甲比乙早到1小时,
(2)设甲车离开A城的距离y与t的关系式为y甲=kt,
把(5,300)代入可求得k=60,
∴y甲=60t,
设乙车离开A城的距离y与t的关系式为y乙=mt+n,
把(1,0)和(4,300)代入可得
![]() ,
,
解得:![]() ,
,
∴y乙=100t-100,
令y甲=y乙,可得:60t=100t-100,
解得:t=2.5,
即甲、乙两直线的交点横坐标为t=2.5,
∴甲车出发2.5小时与乙车相遇
(3)当y甲- y乙=20时
60t-100t+100=20,t=2
当y乙- y甲=20时
100t-100-60t=20,t=3
∴3-2=1(小时)
∴两车都在行驶过程中可以通过无线电通话的时间有1小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线y=3x+m经过第一、三、四象限,则抛物线y=(x-m)
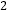 +1的顶点在第象限( )
+1的顶点在第象限( )
A.一
B.二
C.三
D.四 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=kx+k,与y=
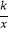 在同一坐标系中的图象大致如图,则( )
在同一坐标系中的图象大致如图,则( )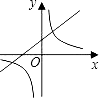
A.K﹥0
B.K﹤0
C.-1﹤K﹤0
D.K﹤-1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为线段AD上一点,CO⊥AD于点O,OA=OB,OC=OD,点M、N分别是AC、BD的中点,连接OM、ON、MN.
(1)求证:AC=BD;
(2)试判断△MON的形状,并说明理由;
(3)若AC=2,在图2中,点M在DB的延长线上,求△AMD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=x
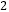 -4x+c的图象与x轴没有交点,其中c为常数,则C的取值范围 是( )
-4x+c的图象与x轴没有交点,其中c为常数,则C的取值范围 是( )
A.c<4
B.c≤4
C.c﹥4
D.c≥4 -
科目: 来源: 题型:
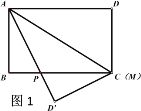
查看答案和解析>>【题目】已知长方形ABCD中,AD=10cm,AB=6cm,点M在边CD上,由C往D运动,速度为1cm/s,运动时间为t秒,将△ADM沿着AM翻折至△ADM,点D对应点为D,AD所在直线与边BC交于点P.
(1)如图1,当t=0时,求证:PA=PC;
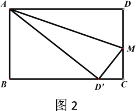
(2)如图2,当t为何值时,点D恰好落在边BC上;
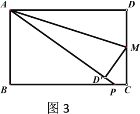
(3)如图3,当t=3时,求CP的长.
 (
( -
科目: 来源: 题型:
查看答案和解析>>【题目】甲组的
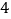 名工人12月份完成的总工作量比此月人均定额的
名工人12月份完成的总工作量比此月人均定额的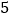 倍多
倍多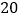 件,乙组的
件,乙组的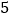 名工人12月份完成的总工作量比此月人均定额的
名工人12月份完成的总工作量比此月人均定额的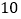 倍少
倍少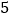 件.
件.(1)如果两组工人实际完成的此月人均工作量相等,那么此月的人均定额是多少件?
(2)如果甲组工人实际完成的此月人均工作量比乙组工人实际完成的此月人均工作量少3件,那么此月人均定额是多少件?
相关试题

