【题目】某校两次购买足球和篮球的支出情况如表:
足球(个) | 篮球(个) | 总支出(元) | |
第一次 | 2 | 3 | 310 |
第二次 | 5 | 2 | 500 |
(1)求购买一个足球、一个篮球的花费各需多少元?(请列方程组求解)
(2)学校准备给帮扶的贫困学校送足球、篮球共计60个,恰逢市场对两种球的价格进行了调整,足球售价提高了10%,篮球售价降低了10%,如果要求一次性购得这批球的总费用不超过4000元,那么最多可以购买多少个足球?
参考答案:
【答案】(1)80和50;(2)30.
【解析】
(1)设购买一个足球需x元,购买一个篮球需y元,根据表格所给数据列出方程解答即可;
(2)设购买a个足球,根据题意列出不等式解答即可
解:(1)设购买一个足球需要x元,购买一个篮球的花费需要y元,
根据题意,得![]() ,
,
解得:![]() .
.
答:购买一个足球和一个篮球的花费各需要80和50元;
(2)设购买a个足球,根据题意,得:
(1+10%)×80a+(1﹣10%)×50(60﹣a)≤4000,
解得:a≤![]() ,
,
又∵a为正整数,
∴a的最大值为30.
答:最多可以购买30个足球.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在半圆O上,半径OB=2
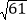 ,AD=10,点C在弧BD上移动,连接AC,H是AC上一点,∠DHC=90°,连接BH,点C在移动的过程中,BH的最小值是( )
,AD=10,点C在弧BD上移动,连接AC,H是AC上一点,∠DHC=90°,连接BH,点C在移动的过程中,BH的最小值是( )
A. 5B. 6C. 7D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,垂足为D,AD=CD,点E在AD上,DE=BD,M、N分别是AB、CE的中点.
(1)求证:△ADB≌△CDE;
(2)求∠MDN的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 都在反比例函数
都在反比例函数 的图象上.
的图象上.(1)求
 的值;
的值;(2)如果
 为
为 轴上一点,
轴上一点, 为
为 轴上一点,以点
轴上一点,以点 为顶点的四边形是平行四边形,试求直线
为顶点的四边形是平行四边形,试求直线 的函数表达式;
的函数表达式;(3)将线段
 沿直线
沿直线 进行对折得到线段
进行对折得到线段 ,且点
,且点 始终在直线
始终在直线 上,当线段
上,当线段 与
与 轴有交点时,则
轴有交点时,则 的取值范围为_______(直接写出答案)
的取值范围为_______(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△BAC为圆O内接三角形,AB=AC,D为⊙O上一点,连接CD、BD,BD与AC交于点E,且BC2=ACCE
①求证:∠CDB=∠CBD;
②若∠D=30°,且⊙O的半径为3+
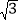 ,I为△BCD内心,求OI的长.
,I为△BCD内心,求OI的长.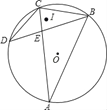
-
科目: 来源: 题型:
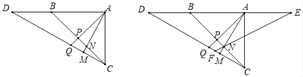
查看答案和解析>>【题目】如图,△ABC中,∠BAC=90°,∠ABC=45°,点D为AB延长线上一点,连接CD,∠AMC=90°,AM交BC于点N,∠APB=90°,AP交CD于点Q.
(1)求证:AN=CQ;
(2)如图,点E在BA的延长线上,且AD=BE,连接EN并延长交CD于点F,求证:DQ=EN;
(3)在(2)的条件下,当3AE=2AB时,请直接写出EN:FN的值为 .
-
科目: 来源: 题型:
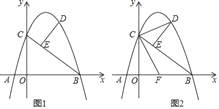
查看答案和解析>>【题目】如图,A(﹣1,0),B(4,0),C(0,3)三点在抛物线y=ax2+bx+c上,D为直线BC上方抛物线上一动点,E在CB上,∠DEC=90°
(1)求抛物线的函数表达式;
(2)如图1,求线段DE长度的最大值;
(3)如图2,F为AB的中点,连接CF,CD,当△CDE中有一个角与∠CFO相等时,求点D的横坐标;若不存在,请说明理由.
相关试题

