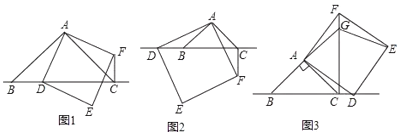
【题目】类比思想就是根据已经学习过的知识,类比探究新知识的思想方法.我们在探究矩形、菱形、正方形等问题中的数量关系时,经常用到类比思想.某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:在![]() 中,
中,![]() 点
点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 重合),以
重合),以![]() 为边在
为边在![]() 右侧作正方形
右侧作正方形![]() 连接
连接![]() .
.
(1)(观察猜想)如图①,当点![]() 在线段
在线段![]() 上时;
上时;
①![]() 与
与![]() 的位置关系为: ;
的位置关系为: ;
②![]() 之间的数量关系为: ;(将结论直接写在横线上)
之间的数量关系为: ;(将结论直接写在横线上)
(2)(数学思考)如图②,当点![]() 在线段
在线段![]() 的延长线上时,结论①②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
的延长线上时,结论①②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
(3)(拓展延伸)如图③,当点![]() 在线段
在线段![]() 的延长线上时,延长
的延长线上时,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .若已知
.若已知![]() 请直接写出
请直接写出![]() 的长.(提示: .过
的长.(提示: .过![]() 作
作![]() 于
于![]() 过
过![]() 作
作![]() 于
于![]() 于
于![]() )
)
参考答案:
【答案】(1)①垂直;![]()
![]() ;(2)结论①成立;结论②不成立,正确结论为:
;(2)结论①成立;结论②不成立,正确结论为:![]() .理由见解析;(3)
.理由见解析;(3)![]() .
.
【解析】
(1)根据正方形的性质得到![]() ,推出
,推出![]() ,根据全等三角形的性质即可得到结论;由正方形
,根据全等三角形的性质即可得到结论;由正方形![]() 的性质可推出
的性质可推出![]() ,根据全等三角形的性质得到
,根据全等三角形的性质得到![]() ,
,![]() ,根据余角的性质即可得到结论;
,根据余角的性质即可得到结论;
(2)根据正方形的性质得到![]() ,推出
,推出![]() ,根据全等三角形的性质以及等腰直角三角形的角的性质可得到结论.
,根据全等三角形的性质以及等腰直角三角形的角的性质可得到结论.
(3)过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() ,如图3所示,由
,如图3所示,由![]() ,推出
,推出![]() ,
,![]() ,推出
,推出![]() ,
,![]() ,由
,由![]() 是等腰直角三角形,推出
是等腰直角三角形,推出![]() ,推出
,推出![]() ,再由勾股定理即可解决问题.
,再由勾股定理即可解决问题.
解:(1)①在正方形![]() 中,
中,![]() ,
,![]()
![]() ,
,
![]()
![]() ,
,
在![]() 与
与![]() 中,
中, ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 即
即![]() ;
;
故答案为:![]() ;
;
②由①知,![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
故答案为:![]() ;
;
(2)![]() 成立;
成立;![]() 不成立,新结论为:
不成立,新结论为:![]() .理由如下:
.理由如下:
在正方形![]() 中,
中,![]() ,
,![]()
![]() ,
,
![]()
![]() ,
,
在![]() 与
与![]() 中,
中, ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,![]() ,
,
![]() .
.
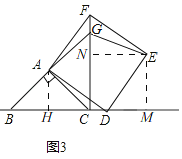
(3)解:如图3,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在正方形![]() 中,
中,![]() ,
,![]()
![]() ,
,
![]()
![]() ,
,
在![]() 与
与![]() 中,
中, ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 即
即![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() .
.
-
科目: 来源: 题型:
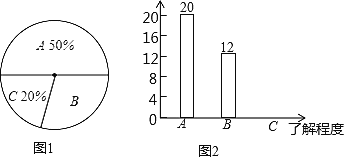
查看答案和解析>>【题目】双峰县教育局要求各学校加强对学生的安全教育,全县各中小学校引起高度重视,小刚就本班同学对安全知识的了解程度进行了一次调查统计.他将统计结果分为三类,A:熟悉;B:了解较多;C:一般了解。图①和图②是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求小刚所在的班级共有多少名学生;
(2)在条形图中,将表示“一般了解”的部分补充完整‘’
(3)在扇形统计图中,计算“了解较多”部分所对应的扇形圆心角的度数;
(4)如果小刚所在年级共1000名同学,请你估算全年级对安全知识“了解较多”的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:
(1) +|1﹣
+|1﹣  |﹣π0+
|﹣π0+ 
(2)( +
+  )×
)×  ﹣(4
﹣(4  ﹣3
﹣3  )÷2
)÷2  .
. -
科目: 来源: 题型:
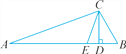
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB于点D,CE是∠ACB的平分线,∠A=20°,∠B=60°,求∠BCD和∠ECD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与计算:请阅读以下材料,并完成相应的任务. 古希腊的几何学家海伦在他的《度量》一书中给出了利用三角形的三边求三角形面积的“海伦公式”:如果一个三角形的三边长分别为a、b、c,设p=
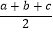 ,则三角形的面积S=
,则三角形的面积S= 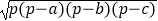 .
.
我国南宋著名的数学家秦九韶,曾提出利用三角形的三边求面积的“秦九韶公式”(三斜求积术):如果一个三角形的三边长分别为a、b、c,则三角形的面积S=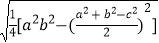 .
.
(1)若一个三角形的三边长分别是5,6,7,则这个三角形的面积等于 .
(2)若一个三角形的三边长分别是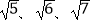 ,求这个三角形的面积.
,求这个三角形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题,原命题和它的逆命题都是真命题的是( )
A.若
 ,则
,则
B.若三角形的三条边分别为
 ,则这个三角形是直角三角形
,则这个三角形是直角三角形C.正方形的四条边都相等
D.对角线互相垂直平分的四边形是菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产A、B两种产品共50件,需购买甲、乙两种材料.生产一件A产品需甲种材料30千克、乙种材料10千克;生产一件B产品需甲、乙两种材料各20千克.经测算,购买甲、乙两种材料各1千克共需资金40元,购买甲种材料2千克和乙种材料3千克共需资金105元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过38000元,且生产B产品不少于28件,问符合条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费200元,生产一件B产品需加工费300元,应选择哪种生产方案,使生产这50件产品的成本最低?(成本=材料费+加工费)
相关试题

