【题目】如图,抛物线与直线都经过坐标轴的正半轴上A(4,0),B两点,该抛物线的对称轴x=﹣1,与x轴交于点C,且∠ABC=90°,求:
(1)直线AB的解析式;
(2)抛物线的解析式.

参考答案:
【答案】(1)y=﹣![]() x+2;(2)y=﹣
x+2;(2)y=﹣![]() x2﹣
x2﹣![]() x+2;
x+2;
【解析】
(1)先证明Rt△CBO∽Rt△BAO,利用相似比计算出OB=2,则B点坐标为(0,2),然后利用待定系数法确定直线AB的解析式;
(2)先利用对称性得到抛物线与x轴的另一个交点坐标为(-6,0),则可设交点式y=a(x+6)(x-4),然后把B点坐标代入求出a即可.
(1)∵A点坐标为(4,0),C点坐标为(﹣1,0),
∴OA=4,OC=1,
∵∠ABC=90°,
∴∠CBO=∠BAO,
∴Rt△CBO∽Rt△BAO,
∴OB:OA=OC:OB,即OB:4=1:OB,
∴OB=2,
∴B点坐标为(0,2),
设直线AB的解析式为y=mx+n,
把A(4,0)、B(0,2)代入得![]() ,解得
,解得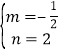 ,
,
∴直线AB的解析式为y=﹣![]() x+2;
x+2;
(2)∵该抛物线的对称轴x=﹣1,
而A点坐标为(4,0),
∴抛物线与x轴的另一个交点坐标为(﹣6,0),
设抛物线的解析式为y=a(x+6)(x﹣4),
把B(0,2)代入得a6(﹣4)=2,解得a=﹣![]() ,
,
所以抛物线的解析式为y=﹣![]() (x+6)(x﹣4)=﹣
(x+6)(x﹣4)=﹣![]() x2﹣
x2﹣![]() x+2.
x+2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
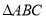 中,
中,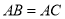 ,
,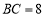 ,点
,点 从点
从点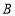 出发沿射线
出发沿射线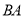 移动,同时点
移动,同时点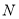 从点
从点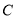 出发沿线段
出发沿线段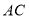 的延长线移动,点
的延长线移动,点 ,
,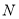 移动的速度相同,
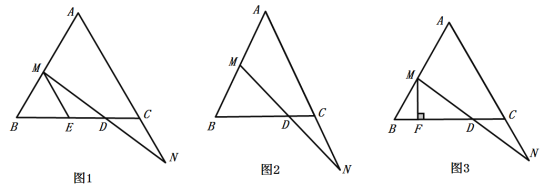
移动的速度相同,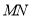 与
与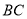 相交于点
相交于点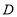 .
.
(1)如图1,过点
 作
作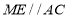 ,交
,交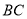 于点
于点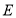 ,求证:
,求证: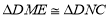 ;
;(2)如图2,
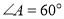 ,当点
,当点 移动到
移动到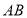 的中点时,求
的中点时,求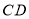 的长度;
的长度;(3)如图3,过点
 作
作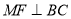 于点
于点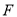 .在点
.在点 从点
从点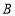 向点
向点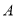 (点
(点 不与点
不与点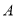 ,
,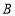 重合)移动的过程中,线段
重合)移动的过程中,线段 与
与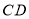 的长度是否保持不变若保持不变,请求出
的长度是否保持不变若保持不变,请求出 与
与 的长度和;若改变,请说明理由.
的长度和;若改变,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)2x2+4x﹣3=0(配方法解)
(2)5x2﹣8x+2=0(公式法解)
(3)3(x﹣5)2=2(5﹣x)
(4)(3x+2)(x+3)=x+14.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利45元,为了扩大销售、增加盈利尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件,若商场平均每天盈利2100元,每件衬衫应降价多少元?请完成下列问题:
(1)未降价之前,某商场衬衫的总盈利为 元.
(2)降价后,设某商场每件衬衫应降价x元,则每件衬衫盈利 元,平均每天可售出 件(用含x的代数式进行表示)
(3)请列出方程,求出x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,则∠AEB的度数为__________.
(2)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.

相关试题

