【题目】其工厂甲.乙两个部门各有员工![]() 人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从甲、乙两个部门各随机抽取![]() 名员工进行了生产技能测试,测试成绩(百分制)如下:
名员工进行了生产技能测试,测试成绩(百分制)如下:
甲:78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙:93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
(1)按如下分数段整理、描述这两组样本数据:
成绩人数部门 |
|
|
|
|
|
|
甲 |
|
|
|
|
|
|
乙 |
(说明:成绩![]() 分及以上为生产技能优秀,
分及以上为生产技能优秀,![]() 分为生产技能良好,
分为生产技能良好,![]() 分为生产技能合格,
分为生产技能合格,![]() 分以下为生产技能不合格)
分以下为生产技能不合格)
(2)若按照甲部门的样本数据,在列频数分布表时,若取组距为![]() ,则
,则![]() 这小组的频数为 ,频率为 ;
这小组的频数为 ,频率为 ;
(3)若按照乙部门的样本数据画出扇形统计图,则表示生产技能优秀部分的圆心角是 度;
得出结论:
(4)估计乙部门生产技能优秀的员工人数为 ;
(5)可以推断出部门员工的生产技能水平较高,你的理由为 (说出一条即可)
参考答案:
【答案】(1)1,0,0,7,10,2;(2)11,55%;(3)216;(4)240人;(5)乙部门,乙部门优秀所占的百分比较大,到达![]() .(答案不唯一,言之有理即可.)
.(答案不唯一,言之有理即可.)
【解析】
(1)分别统计各组的频数填入表格即可;
(2)通过频数分布表得出频数,计算频率,从而得出答案;
(3)先求出乙部门生产技能优秀占乙部门人数的百分比,然后再与360°相乘即可求得度数;
(4)样本估计总体,样本中优秀所占的百分比为![]() ,于是估计总体中优秀所占的百分比也为
,于是估计总体中优秀所占的百分比也为![]() ,进而求出优秀人数;
,进而求出优秀人数;
(5)通过优秀所占的比例,做出判断.
解:(1)按如下分数段整理、描述这两组样本数据:

(2)通过频数分布表可得,![]() 有11人,调查人数20人,频率为
有11人,调查人数20人,频率为![]() ,
,
故答案为:11,![]() ,
,
(3)乙部门画出扇形统计图,则表示生产技能优秀部分的圆心角为:![]() ,
,
故答案为:216.
(4)![]() 人,
人,
故答案为:240
(5)乙部门,理由:乙部门优秀所占的百分比较大,到达![]() .
.
故答案为:乙部门,乙部门优秀所占的百分比较大,到达![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD⊥BC,EG⊥BC,垂足分别为D、G、AD平分∠BAC,求证:∠E=∠4.
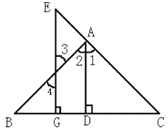
证明:∵AD⊥BC,EG⊥BC(已知)
∴AD∥EG( )
∴∠2=∠3( )
∠1= (两直线平行,同位角相等)
∵AD平分∠BAC(已知)
∴∠1=∠2( )
∴∠E=∠3( )
∵∠3=∠4( )
∴∠E=∠4(等量代换)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠3=∠B.
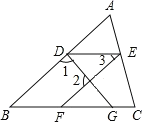
(1)DE与BC平行吗?为什么?
(2)若ED平分∠AEF,∠C=45°,试判定EF与AC有怎样的位置关系?并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字.现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y).
(1)请用列表或画树状图的方法写出所有可能得到的点P的坐标;
(2)计算点P在函数y=
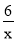 图象上的概率.
图象上的概率.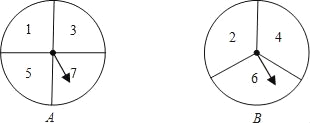
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,三角形ABC的顶点都在网格点上,C点的坐标为(1,2).

(1)直接写出点A、B的坐标.
(2)点P(a,b)是△ABC内任意一点,把△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'C',点P的对应点为P',则点P'的坐标是 .
(3)求三角形ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 两地相距
两地相距 ,甲、乙二人分别骑自行车和摩托车沿相同路线匀速行驶,由
,甲、乙二人分别骑自行车和摩托车沿相同路线匀速行驶,由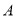 地到达
地到达 地.他们行驶的路程
地.他们行驶的路程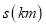 与甲出发后的时间
与甲出发后的时间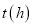 之间的函数图像如图所示.
之间的函数图像如图所示.(1)乙比甲晚出发几小时?乙比甲早到几小时?
(2)分别写出甲、乙行驶的路程
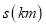 与甲出发后的时间
与甲出发后的时间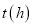 的函数关系式(不写自变量的取值范围).
的函数关系式(不写自变量的取值范围).(3)乙在甲出发后几小时追上甲?追上甲的地点离
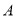 地有多远?
地有多远?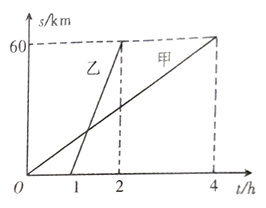
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,2),且
 +(a+2b-4)2=0.
+(a+2b-4)2=0.(1)求a,b的值.
(2)在y轴的正半轴上存在一点M,使S△COM=
 S△ABC,求出点M的坐标.
S△ABC,求出点M的坐标.(3)在坐标轴的其他位置是否有在点M,使S△COM=
 S△ABC仍成立?若存在,请直 接写出符合条件的点M的坐标.
S△ABC仍成立?若存在,请直 接写出符合条件的点M的坐标.
相关试题

