【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,2),且![]() +(a+2b-4)2=0.
+(a+2b-4)2=0.
(1)求a,b的值.
(2)在y轴的正半轴上存在一点M,使S△COM=![]() S△ABC,求出点M的坐标.
S△ABC,求出点M的坐标.
(3)在坐标轴的其他位置是否有在点M,使S△COM=![]() S△ABC仍成立?若存在,请直 接写出符合条件的点M的坐标.
S△ABC仍成立?若存在,请直 接写出符合条件的点M的坐标.

参考答案:
【答案】(1)a=2,b=3;(2)(0,5);(3)(0,-5)或(-2.5,0)或(2.5,0).
【解析】
(1)根据非负数的性质列出关于a、b的二元一次方程组,求解即可;
(2)根据三角形的面积公式列式求出OM的长,然后写出点M的坐标即可;
(3)写出点M在y轴负半轴上时的坐标,再求出点M在x轴上,根据三角形的面积公式列式求出OM的长,然后写出点M的坐标.
解:(1)由题意得,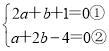 ,
,
①×2得,4a+2b+2=0③,
③②得,3a=6,
解得a=2,
把a=2代入①得,4+b+1=0,
解得b=3;
(2)∵a=2,b=3,C(1,2),
∴AB=3(2)=5,点C到y轴的距离为1,
∴![]() OM1=
OM1=![]() ×
×![]() ×5×2,
×5×2,
解得OM=5,
∵点M在y轴正半轴上,
∴M的坐标为(0,5);
(3)存在.
点M在y轴负半轴上时,点M(0,-5),
点M在x轴上时,![]() OM2=
OM2=![]() ×
×![]() ×5×2,
×5×2,
解得OM=2.5,
所以,点M的坐标为(-2.5,0)或(2.5,0),
综上所述,存在点M的坐标为(0,-5)或(-2.5,0)或(2.5,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】其工厂甲.乙两个部门各有员工
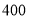 人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.收集数据
从甲、乙两个部门各随机抽取
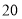 名员工进行了生产技能测试,测试成绩(百分制)如下:
名员工进行了生产技能测试,测试成绩(百分制)如下:甲:78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙:93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
(1)按如下分数段整理、描述这两组样本数据:
成绩人数部门
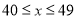
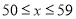
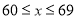
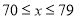
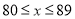
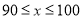
甲
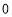
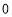
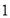
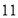
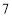
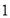
乙
(说明:成绩
 分及以上为生产技能优秀,
分及以上为生产技能优秀,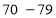 分为生产技能良好,
分为生产技能良好,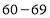 分为生产技能合格,
分为生产技能合格,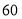 分以下为生产技能不合格)
分以下为生产技能不合格)(2)若按照甲部门的样本数据,在列频数分布表时,若取组距为
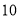 ,则
,则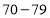 这小组的频数为 ,频率为 ;
这小组的频数为 ,频率为 ;(3)若按照乙部门的样本数据画出扇形统计图,则表示生产技能优秀部分的圆心角是 度;
得出结论:
(4)估计乙部门生产技能优秀的员工人数为 ;
(5)可以推断出部门员工的生产技能水平较高,你的理由为 (说出一条即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,三角形ABC的顶点都在网格点上,C点的坐标为(1,2).

(1)直接写出点A、B的坐标.
(2)点P(a,b)是△ABC内任意一点,把△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'C',点P的对应点为P',则点P'的坐标是 .
(3)求三角形ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 两地相距
两地相距 ,甲、乙二人分别骑自行车和摩托车沿相同路线匀速行驶,由
,甲、乙二人分别骑自行车和摩托车沿相同路线匀速行驶,由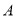 地到达
地到达 地.他们行驶的路程
地.他们行驶的路程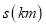 与甲出发后的时间
与甲出发后的时间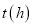 之间的函数图像如图所示.
之间的函数图像如图所示.(1)乙比甲晚出发几小时?乙比甲早到几小时?
(2)分别写出甲、乙行驶的路程
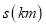 与甲出发后的时间
与甲出发后的时间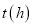 的函数关系式(不写自变量的取值范围).
的函数关系式(不写自变量的取值范围).(3)乙在甲出发后几小时追上甲?追上甲的地点离
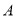 地有多远?
地有多远?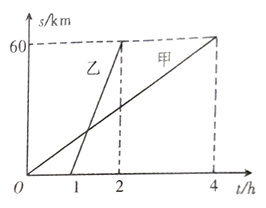
-
科目: 来源: 题型:
查看答案和解析>>【题目】小东根据学习一次函数的经验,对函数y=|2x﹣1|的图象和性质进行了探究.下面是小东的探究过程,请补充完成:
(1)函数y=|2x﹣1|的自变量x的取值范围是 ;
(2)已知:
①当x=
 时,y=|2x﹣1|=0;
时,y=|2x﹣1|=0; ②当x>
 时,y=|2x﹣1|=2x﹣1
时,y=|2x﹣1|=2x﹣1③当x<
 时,y=|2x﹣1|=1﹣2x;
时,y=|2x﹣1|=1﹣2x;显然,②和③均为某个一次函数的一部分.
(3)由(2)的分析,取5个点可画出此函数的图象,请你帮小东确定下表中第5个点的坐标(m,n),其中m= ;n= ;:
x
…
﹣2
0

1
m
…
y
…
5
1
0
1
n
…
(4)在平面直角坐标系xOy中,作出函数y=|2x﹣1|的图象;
(5)根据函数的图象,写出函数y=|2x﹣1|的一条性质.

-
科目: 来源: 题型:
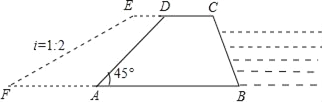
查看答案和解析>>【题目】如图,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45°的防洪大堤(横截面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF的坡比i=1:2.
(1)求加固后坝底增加的宽度AF的长;
(2)求完成这项工程需要土石多少立方米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,点D、E分别在AB、AC上,要得到△ABE≌△ACD,可添加条件( )

A. ∠A=∠AB. ∠ABC=∠ACBC. BE=CDD. AD=AE
相关试题

