【题目】已知a是最大的负整数,![]() ,c是-4的相反数,且a,b,c分别是点A.B.C在数轴上对应的数.
,c是-4的相反数,且a,b,c分别是点A.B.C在数轴上对应的数.

(1)求a,b,c的值,并在数轴上标出点A,B,C;
(2)在数轴上,若D到A的距离刚好是3,则D点叫做A的“幸福点”.则A的幸福点D所表示的数应该是_______________.
(3)若动点P从点B出发沿数轴向正方向运动,动点Q同时从点A出发也沿数轴向正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度,求运动几秒后,点P可以追上点Q?
(4)在数轴上,若M到A,C的距离之和为6,则M叫做A,C的“幸福中心”.请直接写出所有点M在数轴上对应的数.
参考答案:
【答案】(1)![]() ,图见解析;
,图见解析;
(2)-4或2;
(3)运动2秒后,点P可以追上点Q;
(4)点M对应的数是-1.5或4.5.
【解析】
(1)根据有理数的有相关概念可直接得出,并在数轴上表示出来即可;
(2)根据数轴上的点表示数的方法可得出点D表示的数有两种可能,分情况写出即可;
(3)设运动t秒后,点P可以追上点Q,根据题意列出方程求解即可;
(4)分点M在点A左边,AC之间和点C右边三种情况讨论列出方程可得解.
解:(1)由题意得:![]() ,
,
数轴上表示如下图:

(2)当D在A左边时,D表示的数为-4,
当D在A右边时,D表示的数为2,
故答案为-4或2;
(3)设运动t秒后,点P可以追上点Q,
则点P表示数-5+3t,点Q表示t-1,
依题意得:-5+3t=t-1,
解得:t=2.
答:运动2秒后,点P可以追上点Q;
(4)设点M表示的数是m,分点M在点A左边,A、C之间和点C右边三种情况讨论.
当M在点A左边时,AM=-1-m,CM=4-m,
-1-m+4-m=6,解得m=-1.5;
当M在点A、C之间时,AM+CM=AC=5,故此时m无解;
当M在点C右边时,AM=m+1,CM=m-4,
m+1+ m-4=6. 解得m=4.5;
故使点M到A、C的距离之和等于6,点M对应的数是-1.5或4.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC中,BF是AC边上中线,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,当△AEF周长最小时,∠CFE的大小是( )

A. 30° B. 45° C. 60° D. 90°
-
科目: 来源: 题型:
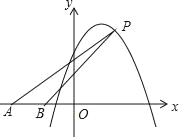
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(﹣5,0)、(﹣2,0).点P在抛物线y=﹣2x2+4x+8上,设点P的横坐标为m.当0≤m≤3时,△PAB的面积S的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据:x1,x2,x3,x4,x5,x6的平均数是2,方差是3,则另一组数据:3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2,3x6﹣2的平均数和方差分别是( )
A. 2,3 B. 2,9 C. 4,25 D. 4,27
-
科目: 来源: 题型:
查看答案和解析>>【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
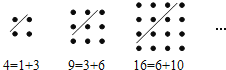
A.13=3+10B.25=9+16C.36=15+21D.49=18+31
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)-3-7;
(2)
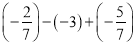 ;
;(3)-0.5+(-15.5)-(-17)-|-12|;
(4)
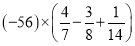 ;
;(5)
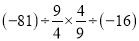 ;
; (6)
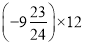 (用简便方法计算).
(用简便方法计算). -
科目: 来源: 题型:
查看答案和解析>>【题目】ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
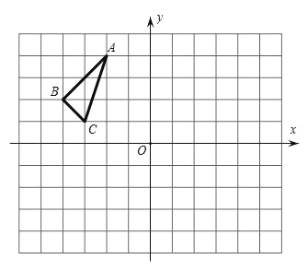
(1)画出ABC关于原点O的中心对称图形A1B1C1,并写出点A1的坐标;
(2)将ABC绕点C顺时针旋转90得到A2B2C,画出A2B2C,求在旋转过程中,线段CA所扫过的面积.
相关试题

