【题目】如图,在□ABCD中,F是AD的中点,延长BC到点E,使CE=![]() BC,连结DE,CF。
BC,连结DE,CF。

(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长。
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)由“平行四边形的对边平行且相等”的性质推知AD∥BC,且AD=BC;然后根据中点的定义、结合已知条件推知四边形CEDF的对边平行且相等(DF=CE,且DF∥CE),即四边形CEDF是平行四边形;
(2)如图,过点D作DH⊥BE于点H,构造含30度角的直角△DCH和直角△DHE.通过解直角△DCH和在直角△DHE中运用勾股定理来求线段ED的长度.
试题解析:(1)证明:在ABCD中,AD∥BC,且AD=BC.
∵F是AD的中点,
∴DF=![]() AD.
AD.
又∵CE=![]() BC,
BC,
∴DF=CE,且DF∥CE,
∴四边形CEDF是平行四边形;
如图,过点D作DH⊥BE于点H.
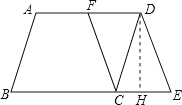
在ABCD中,∵∠B=60°,
∴∠DCE=60°.
∵AB=4,
∴CD=AB=4,
∴CH=![]() CD=2,DH=2
CD=2,DH=2![]() .
.
在CEDF中,CE=DF=![]() AD=3,则EH=1.
AD=3,则EH=1.
∴在Rt△DHE中,根据勾股定理知DE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点A(-3,4)、B(-3,0)、C(-1,0) .以D为顶点的抛物线y = ax2+bx+c过点B. 动点P从点D出发,沿DC边向点C运动,同时动点Q从点B出发,沿BA边向点A运动,点P、Q运动的速度均为每秒1个单位,运动的时间为t秒. 过点P作PE⊥CD交BD于点E,过点E作EF⊥AD于点F,交抛物线于点G.

(1)求抛物线的解析式;
(2)当t为何值时,四边形BDGQ的面积最大?最大值为多少?
(3)动点P、Q运动过程中,在矩形ABCD内(包括其边界)是否存在点H,使以B,Q,E,H为顶点的四边形是菱形,若存在,请直接写出此时菱形的周长;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|﹣3|+(﹣2)3+10=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台.若商店保持两种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从2,3,4,5,6中任取两个数就组成一组数,其中两数之和小于10的数组共有 组.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣3.5,
 ,0,
,0,  ,﹣
,﹣ 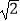 ,
,  ,0.161161116…中,无理数有( )个.
,0.161161116…中,无理数有( )个.
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】质量检测部门对甲、乙两工厂生产的同样产品抽样调查,计算出甲厂的样本方差为0.99,乙厂的样本方差为1.22.由此可以推断出生产此类产品,质量比较稳定的是_____厂.
相关试题

