【题目】如图，在平面直角坐标系中，已知矩形ABCD的三个顶点A(－3，4)、B(－3，0)、C(－1，0) .以D为顶点的抛物线y = ax2+bx+c过点B. 动点P从点D出发，沿DC边向点C运动，同时动点Q从点B出发，沿BA边向点A运动，点P、Q运动的速度均为每秒1个单位，运动的时间为t秒. 过点P作PE⊥CD交BD于点E，过点E作EF⊥AD于点F，交抛物线于点G.

（1）求抛物线的解析式；

（2）当t为何值时，四边形BDGQ的面积最大？最大值为多少？

（3）动点P、Q运动过程中，在矩形ABCD内（包括其边界）是否存在点H，使以B，Q，E，H为顶点的四边形是菱形，若存在，请直接写出此时菱形的周长；若不存在，请说明理由.

参考答案：

【答案】（1）y=－x2－2x＋3（2）当t =2时，四边形BDGQ的面积最大，最大值为2（3）存在， 或80－32

【解析】试题分析：（1）根据矩形的性质可以写出点D得到坐标；由顶点D的坐标可设该抛物线的顶点式方程为y=a（x+1）2+4，然后将点B的坐标代入，即可求得系数a的值（利用待定系数法求抛物线的解析式）。（2）利用三角形相似△DPE∽△DBC可以求得点E的横坐标，再求出AF的长，将其代入抛物线求出点G的横坐标；然后结合抛物线方程、图形与坐标变换可以求得GE=最后根据三角形的面积公式可以求得，S四边形BDGQ= S△BQG＋S△BEG＋S△DEG，由二次函数的最值可以解得t=2时，S△ACG的最大值为2;（3）因为菱形是邻边相等的平行四边形，所以点H在直线EF上。分CE是边和对角线两种情况讨论即可。

试题解析：

（1） 由题意得，顶点D点的坐标为（－1，4）.

设抛物线的解析式为y=a (x＋1) 2＋4（a≠0），

∵抛物线经过点B(－3，0)，代入y=a (x＋1) 2＋4

可求得a=－1

∴抛物线的解析式为y=－ (x＋1) 2＋4

即y=－x2－2x＋3.

（2）由题意知，DP=BQ = t，

∵PE∥BC，

∴△DPE∽△DBC.

∴=2，

∴PE=DP= t.

∴点E的横坐标为－1－t，AF=2－t.

将x =－1－t代入y=－ (x＋1) 2＋4，得y=－t2＋4.

∴点G的纵坐标为－t2＋4，

∴GE=t2＋4－（4－t）=－t2＋t.

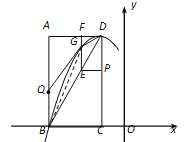
连接BG，S四边形BDGQ= S△BQG＋S△BEG＋S△DEG，

即S四边形BDGQ=BQ·AF＋EG·（AF＋DF）

=t（2－t）－t2＋t.

=－t2＋2t=－ (t－2)2＋2.

∴当t =2时，四边形BDGQ的面积最大，最大值为2.

（3）存在，

菱形BQEH的周长为或80－32.

关闭