【题目】如图,一次函数 ![]() 的图像与反比例函数
的图像与反比例函数 ![]() (
( ![]() 为常数,且
为常数,且 ![]() )的图像都经过点
)的图像都经过点 ![]()

(1)求点 ![]() 的坐标及反比例函数的表达式;
的坐标及反比例函数的表达式;
(2)结合图像直接比较:当 ![]() 时,
时, ![]() 和
和 ![]() 的大小.
的大小.
参考答案:
【答案】
(1)解:将点A(m,2)代入一次函数解析式可得:m+1=2 则m=1 则点A的坐标为(1,2)
将点A(1,2)代入反比例函数解析式可得:k=2 所以反比例函数的解析式为:y= ![]()
(2)解:根据函数图象可得:当 ![]() 时,
时, ![]() ;当
;当 ![]() 时,
时, ![]() ;当
;当 ![]() 时,
时, ![]()
【解析】(1)将A点的坐标代入一次函数的解析式即可求出m的值,从而得出点A的坐标;将点A(1,2)代入反比例函数解析式求出K的值,从而得出反比例函数的解析式;
(2)利用图像比较 y 1 和 y 2 的大小,就是看谁的图像在上方,谁就大,然后写出相应的自变量的取值即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小明设计的“作角的平分线”的尺规作图的过程.
已知:如图1,
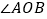 .
.求作:射线
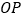 ,使它平分
,使它平分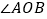 .
.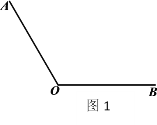
作法:如图2,
①以点
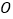 为圆心,任意长为半径作弧,交
为圆心,任意长为半径作弧,交 于点
于点 ,交
,交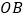 于点
于点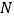 ;
;②分别以点
 ,
,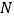 为圆心,以大于
为圆心,以大于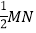 的同样长为半径作弧,两弧交于点
的同样长为半径作弧,两弧交于点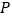 ;
;③作射线
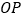 .
.所以射线
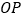 就是所求作的射线.
就是所求作的射线.根据小明设计的尺规作图的过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接
 ,
,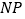 .
.在
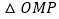 和
和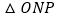 中,
中,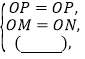
∴
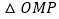 ≌
≌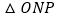 ( )(填推理的依据).
( )(填推理的依据).∴ (全等三角形的 相等).
即射线
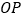 平分
平分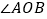 (角平分线定义).
(角平分线定义).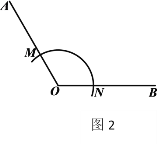
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区为进一步发展基础教育,自
 年以来加大了教育经费的投入,
年以来加大了教育经费的投入, 年该地区投入教育经费
年该地区投入教育经费 万元,
万元, 年投入教育经费
年投入教育经费 万元.
万元.(1)求该地区这两年投入教育经费的年平均增长率;
(2)若该地区教育经费的投入还将保持相同的年平均增长率,请预算
 年该地区投入教育经费为 万元.
年该地区投入教育经费为 万元. -
科目: 来源: 题型:
查看答案和解析>>【题目】当x满足条件
 时,求出方程x2﹣2x﹣4=0的根.
时,求出方程x2﹣2x﹣4=0的根. -
科目: 来源: 题型:
查看答案和解析>>【题目】小红根据学习“数与式”积累的经验,想通过“由特殊到一般”的方法探究下面二次根式的运算规律.
下面是小红的探究过程,请补充完整:
(1)具体运算,发现规律.
特例1:
 ,
,特例2:
 ,
,特例3:
 ,
, 特例4: (填写一个符合上述运算特征的例子).
(2)观察、归纳,得出猜想.
如果
 为正整数,用含
为正整数,用含 的式子表示上述的运算规律为: .
的式子表示上述的运算规律为: .(3)证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, ,
,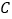 三点在数轴上对应的位置如图如示,其中点
三点在数轴上对应的位置如图如示,其中点 对应的数为2,
对应的数为2, ,
, .
.
(1)点
 对应的数是________,点
对应的数是________,点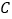 对应的数是________;
对应的数是________;(2)动点
 ,
, 分别同时从
分别同时从 ,
,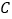 两点出发,分别以每秒8个单位和3个单位的速度沿数轴正方向运动.点
两点出发,分别以每秒8个单位和3个单位的速度沿数轴正方向运动.点 为
为 的中点,点
的中点,点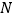 在
在 上,且
上,且 ,设运动时间为
,设运动时间为 .
.①请直接用含
 的代数式表示点
的代数式表示点 ,
,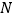 对应的数;
对应的数;②当
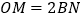 时,求
时,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4 860元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?
相关试题

