【题目】某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4 860元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?
参考答案:
【答案】
(1)解:设平均每次下调的百分率为 ![]() ,则
,则
![]() ,解得:
,解得: ![]() ,
, ![]() (舍去)
(舍去)
∴ 平均每次下调的百分率为10%
(2)解:方案①可优惠:4860×100×(1-0.98)=9720(元),
方案②可优惠:100×80=8000(元),∴ 方案①更优惠.
【解析】(1)设平均每次下调的百分率为 x,这是一道平均降低率的问题,利用公式a(1-x)n=p,(其中a是降低开始的量,n是降低次数,p是降低结束达到的量)列出方程求解检验即可;
(2)分别计算出方案①可优惠的钱数与方案②可优惠的钱数,再进行比较即可得出结论。
【考点精析】认真审题,首先需要了解直接开平方法(方程没有一次项,直接开方最理想.如果缺少常数项,因式分解没商量.b、c相等都为零,等根是零不要忘.b、c同时不为零,因式分解或配方,也可直接套公式,因题而异择良方).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图像与反比例函数
的图像与反比例函数  (
(  为常数,且
为常数,且  )的图像都经过点
)的图像都经过点 

(1)求点 的坐标及反比例函数的表达式;
的坐标及反比例函数的表达式;
(2)结合图像直接比较:当 时,
时,  和
和  的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】小红根据学习“数与式”积累的经验,想通过“由特殊到一般”的方法探究下面二次根式的运算规律.
下面是小红的探究过程,请补充完整:
(1)具体运算,发现规律.
特例1:
 ,
,特例2:
 ,
,特例3:
 ,
, 特例4: (填写一个符合上述运算特征的例子).
(2)观察、归纳,得出猜想.
如果
 为正整数,用含
为正整数,用含 的式子表示上述的运算规律为: .
的式子表示上述的运算规律为: .(3)证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, ,
,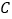 三点在数轴上对应的位置如图如示,其中点
三点在数轴上对应的位置如图如示,其中点 对应的数为2,
对应的数为2, ,
, .
.
(1)点
 对应的数是________,点
对应的数是________,点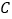 对应的数是________;
对应的数是________;(2)动点
 ,
, 分别同时从
分别同时从 ,
,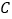 两点出发,分别以每秒8个单位和3个单位的速度沿数轴正方向运动.点
两点出发,分别以每秒8个单位和3个单位的速度沿数轴正方向运动.点 为
为 的中点,点
的中点,点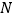 在
在 上,且
上,且 ,设运动时间为
,设运动时间为 .
.①请直接用含
 的代数式表示点
的代数式表示点 ,
,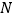 对应的数;
对应的数;②当
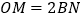 时,求
时,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.

(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;
(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】【概念学习】
规定:求若干个相同的有理数(均不等
 )的除法运算叫做除方,如2÷2÷2,
)的除法运算叫做除方,如2÷2÷2,  等.类比有理数的乘方,我们把
等.类比有理数的乘方,我们把 记作
记作 ,读作“
,读作“ 的圈
的圈 次方”,
次方”,  记作
记作 ,读作“
,读作“ 的圈
的圈 次方”.一般地,把
次方”.一般地,把 (
( )记作
)记作 读作“
读作“ 的圈
的圈 次方”
次方”【初步探究】
(1)直接写出计算结果:
 =_____,
=_____, 
 _____
_____(2)关于除方,下列说法错误的是(______)
A.任何非零数的圈2次方都等于1
B.对于任何正整数
 ,
, 
C.

D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数
【深入思考】
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘法运算呢?


(3)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式
 =_________
=_________(4)想一想:将一个非零有理数
 的圈n次方写成幂的形式等于_________
的圈n次方写成幂的形式等于_________(5)算一算:

-
科目: 来源: 题型:
查看答案和解析>>【题目】创建文明城市,人人参与,人人共建.我市各校积极参与创建活动,自发组织学生走上街头,开展文明劝导活动.某中学九(一)班为此次活动制作了大小、形状、质地等都相同的“文明劝导员”胸章和“文明监督岗”胸章若干,放入不透明的盒中,此时从盒中随机取出“文明劝导员”胸章的概率为
 ;若班长从盒中取出“文明劝导员”胸章3只、“文明监督岗”胸章7只送给九(二)班后,这时随机取出“文明劝导员”胸章的概率为
;若班长从盒中取出“文明劝导员”胸章3只、“文明监督岗”胸章7只送给九(二)班后,这时随机取出“文明劝导员”胸章的概率为  .
.
(1)请你用所学知识计算:九(一)班制作的“文明劝导员”胸章和“文明监督岗”胸章各有多少只?
(2)若小明一次从盒内剩余胸章中任取2只,问恰有“文明劝导员”胸章、“文明监督岗”胸章各1只的概率是多少?(用列表法或树状图计算)
相关试题

