【题目】当x满足条件  时,求出方程x2﹣2x﹣4=0的根.
时,求出方程x2﹣2x﹣4=0的根.
参考答案:
【答案】解:由 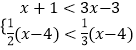 求得
求得 ![]() ,则2<x<4.
,则2<x<4.
解方程x2﹣2x﹣4=0可得x1=1+ ![]() ,x2=1﹣
,x2=1﹣ ![]() ,∵2<
,∵2< ![]() <3,∴3<1+
<3,∴3<1+ ![]() <4,符合题意
<4,符合题意
∴x=1+ ![]() .
.
【解析】分别解出不等式中的每一个不等式,然后利用大小小大中间找得出求出不等式组的解积;然后解出方程x2﹣2x﹣4=0的解,然后根据x的取值范围判断即可。
【考点精析】掌握配方法和一元一次不等式组的解法是解答本题的根本,需要知道左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球每筒的售价多15元,小彬从该网店购买了3筒甲种羽毛球和2筒乙种羽毛球,一共花费270元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定购进甲、乙两种羽毛球各80筒.已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.元旦期间该网店开展优惠促销活动,甲种羽毛球打折销售,乙种羽毛球售价不变,若所购进羽毛球均可全部售出,要使全部售出所购进的羽毛球的利润率是
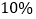 ,那么甲种羽毛球是按原销售价打几折销售的.
,那么甲种羽毛球是按原销售价打几折销售的. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小明设计的“作角的平分线”的尺规作图的过程.
已知:如图1,
 .
.求作:射线
 ,使它平分
,使它平分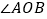 .
.
作法:如图2,
①以点
 为圆心,任意长为半径作弧,交
为圆心,任意长为半径作弧,交 于点
于点 ,交
,交 于点
于点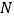 ;
;②分别以点
 ,
,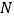 为圆心,以大于
为圆心,以大于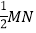 的同样长为半径作弧,两弧交于点
的同样长为半径作弧,两弧交于点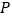 ;
;③作射线
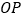 .
.所以射线
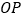 就是所求作的射线.
就是所求作的射线.根据小明设计的尺规作图的过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接
 ,
,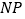 .
.在
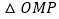 和
和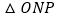 中,
中,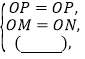
∴
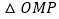 ≌
≌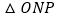 ( )(填推理的依据).
( )(填推理的依据).∴ (全等三角形的 相等).
即射线
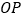 平分
平分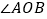 (角平分线定义).
(角平分线定义).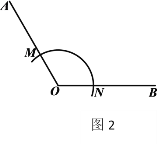
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区为进一步发展基础教育,自
 年以来加大了教育经费的投入,
年以来加大了教育经费的投入, 年该地区投入教育经费
年该地区投入教育经费 万元,
万元, 年投入教育经费
年投入教育经费 万元.
万元.(1)求该地区这两年投入教育经费的年平均增长率;
(2)若该地区教育经费的投入还将保持相同的年平均增长率,请预算
 年该地区投入教育经费为 万元.
年该地区投入教育经费为 万元. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图像与反比例函数
的图像与反比例函数  (
(  为常数,且
为常数,且  )的图像都经过点
)的图像都经过点 

(1)求点 的坐标及反比例函数的表达式;
的坐标及反比例函数的表达式;
(2)结合图像直接比较:当 时,
时,  和
和  的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】小红根据学习“数与式”积累的经验,想通过“由特殊到一般”的方法探究下面二次根式的运算规律.
下面是小红的探究过程,请补充完整:
(1)具体运算,发现规律.
特例1:
 ,
,特例2:
 ,
,特例3:
 ,
, 特例4: (填写一个符合上述运算特征的例子).
(2)观察、归纳,得出猜想.
如果
 为正整数,用含
为正整数,用含 的式子表示上述的运算规律为: .
的式子表示上述的运算规律为: .(3)证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, ,
, 三点在数轴上对应的位置如图如示,其中点
三点在数轴上对应的位置如图如示,其中点 对应的数为2,
对应的数为2, ,
, .
.
(1)点
 对应的数是________,点
对应的数是________,点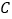 对应的数是________;
对应的数是________;(2)动点
 ,
, 分别同时从
分别同时从 ,
,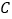 两点出发,分别以每秒8个单位和3个单位的速度沿数轴正方向运动.点
两点出发,分别以每秒8个单位和3个单位的速度沿数轴正方向运动.点 为
为 的中点,点
的中点,点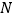 在
在 上,且
上,且 ,设运动时间为
,设运动时间为 .
.①请直接用含
 的代数式表示点
的代数式表示点 ,
,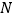 对应的数;
对应的数;②当
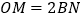 时,求
时,求 的值.
的值.
相关试题

