【题目】小红根据学习“数与式”积累的经验,想通过“由特殊到一般”的方法探究下面二次根式的运算规律.
下面是小红的探究过程,请补充完整:
(1)具体运算,发现规律.
特例1:![]() ,
,
特例2:![]() ,
,
特例3:![]() ,
,
特例4: (填写一个符合上述运算特征的例子).
(2)观察、归纳,得出猜想.
如果![]() 为正整数,用含
为正整数,用含![]() 的式子表示上述的运算规律为: .
的式子表示上述的运算规律为: .
(3)证明你的猜想.
参考答案:
【答案】(1)答案不唯一,如:![]() ;(2)见解析;(3)证明见解析.
;(2)见解析;(3)证明见解析.
【解析】
(1)根据题目中的例子可以写出例4;
(2)根据(1)中特例,可以写出相应的猜想;
(3)根据(2)中的猜想,对等号左边的式子化简,即可得到等号右边的式子,从而可以解答本题.
(1)答案不唯一,如:![]() .
.
(2)![]() (
(![]() 为正整数).
为正整数).
或:![]() (
(![]() 为正整数且
为正整数且![]() ).
).
或:![]() (
(![]() 为正整数且
为正整数且![]() ).
).
(3)证明:∵左边![]() .
.
∵![]() 为正整数,
为正整数,
∴![]() .
.
∴左边![]() .
.
又∵右边![]() ,
,
∴左边=右边.
即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区为进一步发展基础教育,自
 年以来加大了教育经费的投入,
年以来加大了教育经费的投入, 年该地区投入教育经费
年该地区投入教育经费 万元,
万元, 年投入教育经费
年投入教育经费 万元.
万元.(1)求该地区这两年投入教育经费的年平均增长率;
(2)若该地区教育经费的投入还将保持相同的年平均增长率,请预算
 年该地区投入教育经费为 万元.
年该地区投入教育经费为 万元. -
科目: 来源: 题型:
查看答案和解析>>【题目】当x满足条件
 时,求出方程x2﹣2x﹣4=0的根.
时,求出方程x2﹣2x﹣4=0的根. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图像与反比例函数
的图像与反比例函数  (
(  为常数,且
为常数,且  )的图像都经过点
)的图像都经过点 

(1)求点 的坐标及反比例函数的表达式;
的坐标及反比例函数的表达式;
(2)结合图像直接比较:当 时,
时,  和
和  的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, ,
,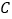 三点在数轴上对应的位置如图如示,其中点
三点在数轴上对应的位置如图如示,其中点 对应的数为2,
对应的数为2, ,
, .
.
(1)点
 对应的数是________,点
对应的数是________,点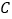 对应的数是________;
对应的数是________;(2)动点
 ,
, 分别同时从
分别同时从 ,
,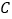 两点出发,分别以每秒8个单位和3个单位的速度沿数轴正方向运动.点
两点出发,分别以每秒8个单位和3个单位的速度沿数轴正方向运动.点 为
为 的中点,点
的中点,点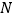 在
在 上,且
上,且 ,设运动时间为
,设运动时间为 .
.①请直接用含
 的代数式表示点
的代数式表示点 ,
,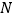 对应的数;
对应的数;②当
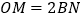 时,求
时,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4 860元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.

(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;
(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
相关试题

