【题目】铁路上![]() 、
、![]() 两点相距25km,
两点相距25km,![]() 为良村庄,
为良村庄,![]() 于
于![]() ,
,![]() 于
于![]() ,已知
,已知![]() ,
,![]() ,现在要在铁路
,现在要在铁路![]() 上修建一个土特产收购站
上修建一个土特产收购站![]() .
.

(1)在图![]() 中,若
中,若![]() ,则
,则![]() 战应修建在离
战应修建在离![]() 站多少千米处.
站多少千米处.
(2)在图![]() 中,若
中,若![]() 值最小,则
值最小,则![]() 点应建在哪里,请求出这个最小值.
点应建在哪里,请求出这个最小值.
参考答案:
【答案】(1)10km.(2)AE=15,E应建在距A15千米处.
【解析】
(1)关键描述语:产品收购站E,使得C、D两村到E站的距离相等,在Rt△DAE和Rt△CBE中,设出AE的长,可将DE和CE的长表示出来,列出等式进行求解即可.
(2)根据题意构造直角三角形D′FC,再由勾股定理求解即可.
(1)设AE=xkm,
∵C、D两村到E站的距离相等,∴DE=CE,即DE2=CE2,
由勾股定理,得152+x2=102+(25-x)2,x=10.
故:E点应建在距A站10千米处.
(2)作D点关于AB的对称点D′,连接D′C,再作D′F⊥BC于点F,此时DE+EC最短,

∵DA=15km,CB=10km,A、B两点相距25km,
∴FC=25km,D′F=25km,
根据题意得,![]()
∴BE=10km
∴AE=15km,
∴E应建在距A15千米处.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥AO,交BO于点N,连结ND、BM,设OP=t.

(1)求点M的坐标(用含t的代数式表示);
(2)试判断线段MN的长度是否随点P的位置的变化而改变?并说明理由.
(3)当t为何值时,四边形BNDM的面积最小;
(4)在x轴正半轴上存在点Q,使得△QMN是等腰三角形,请直接写出不少于4个符合条件的点Q的坐标(用含t的式子表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋中装有一红一白2个球,这些球除颜色外都相同,小刚从袋中随机摸出一个球,记下颜色后放回袋中,再从袋中随机摸出一个球,两次都摸到红球的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
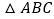 中,
中,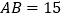 ,
,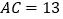 ,高
,高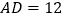 ,则
,则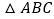 的周长是( ).
的周长是( ).A. 42 B. 32 C. 37或33 D. 42或32
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:“两边及其中一边的对角分别相等的两个三角形不一定全等”.但是,小亮发现:当这两个三角形都是锐角三角形时,它们会全等,除小亮的发现之外,当这两个三角形都是时,它们也会全等;当这两个三角形其中一个三角形是锐角三角形,另一个是时,它们一定不全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示:要设计一副宽20厘米、长30厘米的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2:3,如果要使所有彩条所占面积为原矩形图案面积的
 ,那么横彩条的宽度为多少厘米,竖彩条的宽度为多少厘米?
,那么横彩条的宽度为多少厘米,竖彩条的宽度为多少厘米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点A、B、C在同一直线上,AB=2,BC=1,分别以AB、BC为边,在AC同侧作等边△ABD和等边△BCE,分别联结AE、CD.
(1)找出图中的全等三角形(不添加辅助线),并证明你的结论.

(2)线段AE与线段CD的关系是:AE CD(填>、=、<).AE与CD的夹角是: .
(3) △ABD固定不动,使△BCE绕着点B旋转,①这时(2)得出的结论还成立吗(不要求证明)?
②在旋转过程中,线段DC的长是变化的,它的变化范围是 .
相关试题

