【题目】在一个不透明的袋中装有一红一白2个球,这些球除颜色外都相同,小刚从袋中随机摸出一个球,记下颜色后放回袋中,再从袋中随机摸出一个球,两次都摸到红球的概率是 .
参考答案:
【答案】![]()
【解析】解:画树状图得: 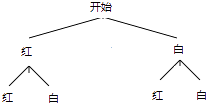
∵共有4种等可能的结果,两次都摸到红球的1种情况,
∴两次都摸到红球的概率是 ![]() ,
,
故答案为 ![]() .
.
先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次都摸到红球的情况,再利用概率公式即可求得答案.此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.
-
科目: 来源: 题型:
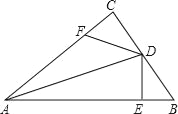
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)请你判断AE、AF与BE之间的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3).
(Ⅰ)求△ABC的面积;
(Ⅱ)在图中作出△ABC关于
 轴的对称图形△A1B1C1,并写出点A1、B1、C1的坐标.
轴的对称图形△A1B1C1,并写出点A1、B1、C1的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥AO,交BO于点N,连结ND、BM,设OP=t.

(1)求点M的坐标(用含t的代数式表示);
(2)试判断线段MN的长度是否随点P的位置的变化而改变?并说明理由.
(3)当t为何值时,四边形BNDM的面积最小;
(4)在x轴正半轴上存在点Q,使得△QMN是等腰三角形,请直接写出不少于4个符合条件的点Q的坐标(用含t的式子表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】在
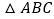 中,
中,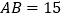 ,
,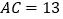 ,高
,高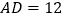 ,则
,则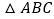 的周长是( ).
的周长是( ).A. 42 B. 32 C. 37或33 D. 42或32
-
科目: 来源: 题型:
查看答案和解析>>【题目】铁路上
 、
、 两点相距25km,
两点相距25km, 为良村庄,
为良村庄, 于
于 ,
, 于
于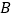 ,已知
,已知 ,
, ,现在要在铁路
,现在要在铁路 上修建一个土特产收购站
上修建一个土特产收购站 .
.
(1)在图
 中,若
中,若 ,则
,则 战应修建在离
战应修建在离 站多少千米处.
站多少千米处.(2)在图
 中,若
中,若 值最小,则
值最小,则 点应建在哪里,请求出这个最小值.
点应建在哪里,请求出这个最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:“两边及其中一边的对角分别相等的两个三角形不一定全等”.但是,小亮发现:当这两个三角形都是锐角三角形时,它们会全等,除小亮的发现之外,当这两个三角形都是时,它们也会全等;当这两个三角形其中一个三角形是锐角三角形,另一个是时,它们一定不全等.
相关试题

