搜索
【题目】某水果店计划进A，B两种水果共140千克，这两种水果的进价和售价如表所示
进价 | 售价 | |
A种水果 | 5 | 8 |
B种水果 | 9 | 13 |
若该水果店购进这两种水果共花费1020元，求该水果店分别购进A，B两种水果各多少千克？
在的基础上，为了迎接春节的来临，水果店老板决定把A种水果全部八折出售，B种水果全部降价
出售，那么售完后共获利多少元？
参考答案：
【答案】(1) 购进A种水果60千克，B种水果80千克;(2)300元.
【解析】
（1）设该水果店购进A种水果x千克，B种水果y千克，根据总价=单价×数量结合花1020元购进A，B两种水果共140千克，即可得出关于x，y的二元一次方程组，解之即可得出结论；
（2）根据利润=销售收入﹣成本，即可求出结论．
（1）设该水果店购进A种水果x千克，B种水果y千克，依题意，得：
解得：
．
答：该水果店购进A种水果60千克，B种水果80千克．
（2）8×0.8×60+13×（1﹣10%）×80﹣1020=300（元）．
答：售完后共获利300元．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）23﹣17﹣（﹣7）+（﹣16）；
（2）-5+6÷（-2）×
；（3）-36×
；（4）﹣23+|5﹣8|+24÷（﹣3）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象，已知探测线与地面的夹角分别是25°和60°，且AB=4米，求该生命迹象所在位置C的深度．（结果精确到1米．参考数据：sin25°≈0.4，cos25°≈0.9，tan25°≈0.5，
≈1.7）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某地电话拨号入网有两种收费方式,用户可以任选其一.
计时制:0.05元/分;
包月制:50元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0.02元/分.
(1)某用户某月上网的时间为x小时,请你分别写出两种收费方式下该用户应该支付的费用.
(2)若某用户估计一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知A、B在数轴上分别表示a、b
（1）对照数轴填写下表：
a
6
-6
-6
-6
-10
-2.5
b
4
0
4
-4
2
-2.5
两点距离
2
6
0
（2）若A、B两点间的距离记为 d，试问d与a、b有何数量关系；
（3）在数轴上找到所有符合条件的整数点P，使它到5和﹣5的距离之和为10，并求出所有这些整数的和；
（4）若数轴上点C表示的数为x，当点C在什么位置时，
①|x+1|的值最小；②|x+1|+|x﹣2|的值最小．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=
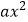+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于C（0，﹣3）．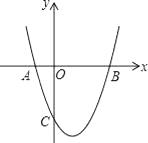
（1）求抛物线的解析式；
（2）D是y轴正半轴上的点，OD=3，在线段BD上任取一点E（不与B，D重合），经过A，B，E三点的圆交直线BC于点F，
①试说明EF是圆的直径；
②判断△AEF的形状，并说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】完成推理过程
（1）如图，已知∠1=∠2，∠B=∠C，求证：AB∥CD．
证明∵∠1=∠2(已知)，
且∠1=∠CGD( )
∴∠2=∠CGD( )，
∴CE∥BF( )，
∴∠C=∠BFD( )
又∵∠B=∠C(已知)，
∴∠BFD=∠B( )，
∴AB∥CD( )
相关试题
