【题目】解方程:
(1)![]() ;
;
(2)用公式法解:4x2﹣3=12x;
(3)![]() .
.
参考答案:
【答案】(1)原分式方程无解;(2)x1=![]() ,x2=
,x2=![]() ;(3)x1=-4,x2=-5.
;(3)x1=-4,x2=-5.
【解析】
(1)方程两边同时乘以最简公分母(x2-1)把分式方程转化为整式方程,解此方程求出x的值,最后检验是否有增根即可得答案;
(2)先把方程整理成一元二次方程的一般形式,再利用一元二次方程的求根公式解方程即可得答案;
(3)先利用多项式乘以多项式法则把括号展开,再整理成一元二次方程的一般形式,最后利用因式分解法解方程即可得答案.
(1)![]()
去分母得:(x+1)2-4=x2-1,
整理得:2x=2,
解得:x=1,
检验:当x=1时,x2-1=0,
∴x=1是原方程的增根,
∴原分式方程无解.
(2)4x2﹣3=12x
4x2-12x-3=0
∵a=4,b=-12,c=-3,
∴△=b2-4ac=![]() >0,
>0,
∴x=![]() =
=![]() ,
,
∴x1=![]() ,x2=
,x2=![]() .
.
(3)![]()
x2+9x+20=0
(x+4)(x+5)=0
x1=-4,x2=-5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.易证:CE=CF.

(1)在图1中,若G在AD上,且∠GCE=45°.试猜想GE,BE,GD三线段之间的数量关系,并证明你的结论.
(2)运用(1)中解答所积累的经验和知识,完成下面两题:
①如图2,在四边形ABCD中∠B=∠D=90°,BC=CD,点E,点G分别是AB边,AD边上的动点.若∠BCD=α,∠ECG=β,试探索当α和β满足什么关系时,图1中GE,BE,GD三线段之间的关系仍然成立,并说明理由.
②在平面直角坐标中,边长为1的正方形OABC的两顶点A,C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图3).设△MBN的周长为p,在旋转正方形OABC的过程中,p值是否有变化?若不变,请直接写出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,
(1)问应将每件售价定为多少元时,才能使每天利润为640元且成本最少?
(2)问应将每件售价定为多少元时,才能使每天利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】课上教师呈现一个问题

甲、乙、丙三位同学用不同的方法添加辅助线解决问题,如下图:
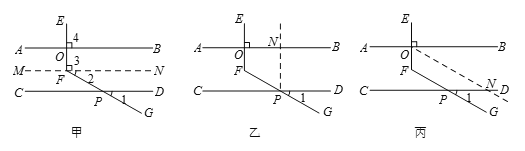
甲同学辅助线的做法和分析思路如下:

(1)请你根据乙同学所画的图形,描述辅助线的做法,并写出相应的分析思路.
辅助线:___________________;
分析思路:
(2)请你根据丙同学所画的图形,求∠EFG的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知长方形ABCD的两个顶点A(2,-1),C(6,2)。点M为y轴上一点,△MAB的面积为6,且MD<MA。
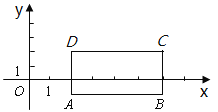
请解答下列问题:
(1)顶点B的坐标为 ;
(2)将长方形ABCD平移后得到
 ,若
,若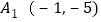 ,则
,则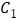 的坐标为 ;
的坐标为 ;(3)求点M的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,△ABC的顶点都在正方形(每个小正方形边长为单位1)网格的格点上.
(1)△ABC的形状是_________(直接写答案);
(2)平移△ABC,若A对应的点A1坐标为(3,﹣1),画出△A1B1C1;
(3)画出△ABC绕点B顺时针旋转90°的△BA2C2并求出线段BC旋转过程扫过的面积.(结果保留π)
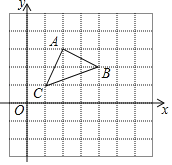
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )
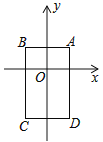
A. (﹣1,﹣2) B. (―1,1)
C. (-1,-1) D. (1,―2)
相关试题

