【题目】课上教师呈现一个问题

甲、乙、丙三位同学用不同的方法添加辅助线解决问题,如下图:
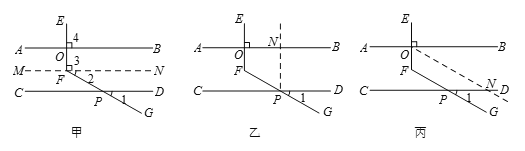
甲同学辅助线的做法和分析思路如下:

(1)请你根据乙同学所画的图形,描述辅助线的做法,并写出相应的分析思路.
辅助线:___________________;
分析思路:
(2)请你根据丙同学所画的图形,求∠EFG的度数.
参考答案:
【答案】(1)辅助线:过点P作PN∥EF交AB于点N.
分析思路:
①欲求∠EFG的度数,由辅助线作图可知,∠EFG=∠NPG,
因此,只需转化为求∠NPG的度数;
②欲求∠NPG的度数,由图可知只需转化为求∠1和∠2的度数;
③又已知∠1的度数,所以只需求出∠2的度数;
④由已知EF⊥AB,可得∠4=90°;
⑤由PN∥EF,可推出∠3=∠4;AB∥CD可推出∠2=∠3,由此可推∠2=∠4,
所以可得∠2的度数;
⑥从而可以求出∠EFG的度数.
(2)120°
【解析】(1)辅助线:过点P作PN∥EF交AB于点N.
分析思路:
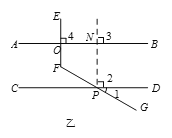
①欲求∠EFG的度数,由辅助线作图可知,∠EFG=∠NPG,
因此,只需转化为求∠NPG的度数;
②欲求∠NPG的度数,由图可知只需转化为求∠1和∠2的度数;
③又已知∠1的度数,所以只需求出∠2的度数;
④由已知EF⊥AB,可得∠4=90°;
⑤由PN∥EF,可推出∠3=∠4;AB∥CD可推出∠2=∠3,由此可推∠2=∠4,
所以可得∠2的度数;
⑥从而可以求出∠EFG的度数.
(2)过点O作ON∥FG
∵ON∥FG
∴∠EFG=∠EON ∠1=∠ONC=30°
∵AB∥CD
∴∠ONC=∠BON=30°
∵EF⊥AB
∴∠EOB=90°
∴∠EFG=∠EON=∠EOB+∠BON=90°+30°=120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠1与∠2是同旁内角,∠1=50,则( )
A. ∠2=50 B. ∠2=130 C. ∠2=50或∠2=130 D. ∠2的大小不确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a2-ka+81是完全平方式,则k=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形两边长分别为3和5,则它的周长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30,再向旗杆的方向前进16米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端A的仰角为45,请计算旗杆AB的高度(结果保留根号).
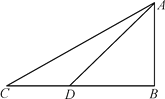
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只蚂蚁从地面开始爬树,它每天不停地往上爬,不幸的是,它每天白天能往上爬3米,可是一到夜里就要滑下2米,但是蚂蚁还是坚持往上爬,这棵树高是20米,蚂蚁从清晨开始从地面往上爬,它需要几天才能爬到树的最高处? ( )
A. 17天 B. 18天 C. 19天 D. 20天
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个等腰三角形的两边分别为4和9,则它的周长是___▲_____ .
相关试题

