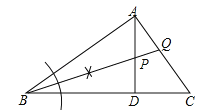
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)求作∠ABC的平分线(要求:尺规作图,保留作图痕迹,不写作法);
(2)若∠ABC的平分线分别交AD,AC于P,Q两点,证明:AP=AQ.

参考答案:
【答案】(1)(2)见解析
【解析】试题分析:(1)作出角平分线BQ即可.
(2)根据余角的定义得出∠AQP+∠ABQ=90°,根据角平分线的性质得出∠ABQ=∠PBD,再由∠BPD=∠APQ可知∠APQ=∠AQP,据此可得出结论.
试题解析:解:(1)BQ就是所求的∠ABC的平分线,P、Q就是所求作的点.
(2)证明:∵AD⊥BC,∴∠ADB=90°,∴∠BPD+∠PBD=90°.
∵∠BAC=90°,∴∠AQP+∠ABQ=90°.
∵∠ABQ=∠PBD,∴∠BPD=∠AQP.
∵∠BPD=∠APQ,∴∠APQ=∠AQP,∴AP=AQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着互联网、移动终端的迅速发展,数字化阅读越来越普及,公交上的“低头族”越来越多.某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(如图1),并将调查结果绘制成图2和图3所示的统计图(均不完整).请根据统计图中提供的信息,解答下列问题:

(1)求出本次接受调查的总人数,并将条形统计图补充完整;
(2)表示观点B的扇形的圆心角度数为度;
(3)2016年底慈溪人口总数约为200万(含外来务工人员),请根据图中信息,估计慈溪市民认同观点D的人数. -
科目: 来源: 题型:
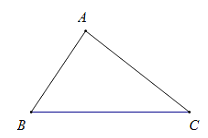
查看答案和解析>>【题目】如图,已知△ABC,按下列要求作图(第(1)、(2)小题用尺规作图,第(3)小题不限作图工具,保留作图痕迹).
(1)作∠B的角平分线;
(2)作BC的中垂线;
(3)以BC边所在直线为对称轴,作△ABC的轴对称图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小轩从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息: ①ab>0;②a+b+c<0;③b+2c>0;④a﹣2b+4c>0;⑤
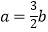 .
.
你认为其中正确信息的个数有( )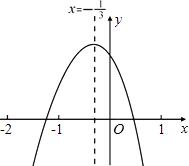
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知△ABC为直角三角形,分别以直角边AC、BC为直径作半圆AmC和BnC,以AB为直径作半圆ACB,记两个月牙形阴影部分的面积之和为S1,△ABC的面积为S2,则S1与S2的大小关系为( )

A. S1>S2 B. S1<S2 C. S1=S2 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两建筑物的水平距离BC为18m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°.则建筑物CD的高度为m(结果不作近似计算).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,BC=3AB,A,B两点的坐标分别是(﹣1,0),(0,2),C,D两点在反比例函数y=
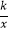 (x<0)的图象上,则k的值等于 .
(x<0)的图象上,则k的值等于 . 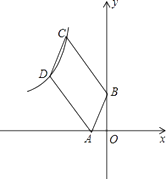
相关试题

