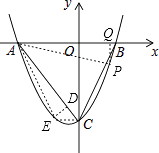
【题目】如图,抛物线y=ax2+bx﹣5(a≠0)与x轴交于点A(﹣5,0)和点B(3,0),与y轴交于点C.
(1)求该抛物线的解析式;
(2)若点E为x轴下方抛物线上的一动点,当S△ABE=S△ABC时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在点P,使∠BAP=∠CAE?若存在,求出点P的横坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:把A、B两点坐标代入解析式可得 ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为y= ![]() x2+
x2+ ![]() x﹣5
x﹣5
(2)
解:在y= ![]() x2+
x2+ ![]() x﹣5中,令x=0可得y=﹣5,
x﹣5中,令x=0可得y=﹣5,
∴C(0,﹣5),
∵S△ABE=S△ABC,且E点在x轴下方,
∴E点纵坐标和C点纵坐标相同,
当y=﹣5时,代入可得 ![]() x2+
x2+ ![]() x=﹣5,解得x=﹣2或x=0(舍去),
x=﹣5,解得x=﹣2或x=0(舍去),
∴E点坐标为(﹣2,﹣5);
(3)
解:假设存在满足条件的P点,其坐标为(m, ![]() m2+
m2+ ![]() m﹣5),
m﹣5),
如图,连接AP、CE、AE,过E作ED⊥AC于点D,过P作PQ⊥x轴于点Q,
则AQ=AO+OQ=5+m,PQ=| ![]() m2+
m2+ ![]() m﹣5|,
m﹣5|,
在Rt△AOC中,OA=OC=5,则AC=5 ![]() ,∠ACO=∠DCE=45°,
,∠ACO=∠DCE=45°,
由(2)可得EC=2,在Rt△EDC中,可得DE=DC= ![]() ,
,
∴AD=AC﹣DC=5 ![]() ﹣
﹣ ![]() =4
=4 ![]() ,
,
当∠BAP=∠CAE时,则△EDA∽△PQA,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴ ![]() m2+
m2+ ![]() m﹣5=
m﹣5= ![]() (5+m)或
(5+m)或 ![]() m2+
m2+ ![]() m﹣5=﹣
m﹣5=﹣ ![]() (5+m),
(5+m),
当 ![]() m2+
m2+ ![]() m﹣5=
m﹣5= ![]() (5+m)时,整理可得4m2﹣5m﹣75=0,解得m=
(5+m)时,整理可得4m2﹣5m﹣75=0,解得m= ![]() 或m=﹣5(与A点重合,舍去),
或m=﹣5(与A点重合,舍去),
当 ![]() m2+
m2+ ![]() m﹣5=﹣
m﹣5=﹣ ![]() (5+m)时,整理可得4m2+11m﹣45=0,解得m=
(5+m)时,整理可得4m2+11m﹣45=0,解得m= ![]() 或m=﹣5(与A点重合,舍去),
或m=﹣5(与A点重合,舍去),
∴存在满足条件的点P,其横坐标为 ![]() 或
或 ![]()
【解析】本题主要考查二次函数的综合运用.涉及到的知识点有待定系数法、三角形的面积、相似三角形的判定和性质及分类讨论等.在(3)中利用∠BAP=∠CAE构造三角形相似是解题的关键.本题考查知识点较多,综合性很强,难度适中.(1)把A、B两点的坐标代入,利用待定系数法可求得抛物线的解析式;(2)当S△ABE=S△ABC时,可知E点和C点的纵坐标相同,可求得E点坐标;(3)在△CAE中,过E作ED⊥AC于点D,可求得ED和AD的长度,设出点P坐标,过P作PQ⊥x轴于点Q,由条件可知△EDA∽△PQA,利用相似三角形的对应边可得到关于P点坐标的方程,可求得P点坐标.
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在国务院办公厅发布《中国足球发展改革总体方案》之后,某校为了调查本校学生对足球知识的了解程度,随机抽取了部分学生进行一次问卷调查,并根据调查结果绘制了如图的统计图,请根据图中所给的信息,解答下列问题:

(1)本次接受问卷调查的学生总人数是;
(2)扇形统计图中,“了解”所对应扇形的圆心角的度数为 , m的值为;
(3)若该校共有学生1500名,请根据上述调查结果估算该校学生对足球的了解程度为“基本了解”的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了经济发展的需要,某市2014年投入科研经费500万元,2016年投入科研经费720万元.
(1)求2014至2016年该市投入科研经费的年平均增长率;
(2)根据目前经济发展的实际情况,该市计划2017年投入的科研经费比2016年有所增加,但年增长率不超过15%,假定该市计划2017年投入的科研经费为a万元,请求出a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.

(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC= ,AB=12,求半圆O所在圆的半径.
,AB=12,求半圆O所在圆的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.

(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.
①求证:△AGE≌△AFE;
②若BE=2,DF=3,求AH的长.
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个公共房门前的台阶高出地面2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( )
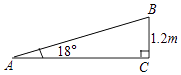
A.斜坡AB的坡度是18°
B.斜坡AB的坡度是tan18°
C.AC=2tan18°米
D.AB=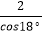 米
米 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A和点B都在反比例函数y=
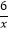 的图象上,且线段AB过原点,过点A作x轴的垂线段,垂足为C,P是线段OB上的动点,连接CP.设△ACP的面积为S,则下列说法正确的是( )
的图象上,且线段AB过原点,过点A作x轴的垂线段,垂足为C,P是线段OB上的动点,连接CP.设△ACP的面积为S,则下列说法正确的是( ) 
A.S>3
B.S>6
C.3≤S≤6
D.3<S≤6
相关试题

