【题目】为了经济发展的需要,某市2014年投入科研经费500万元,2016年投入科研经费720万元.
(1)求2014至2016年该市投入科研经费的年平均增长率;
(2)根据目前经济发展的实际情况,该市计划2017年投入的科研经费比2016年有所增加,但年增长率不超过15%,假定该市计划2017年投入的科研经费为a万元,请求出a的取值范围.
参考答案:
【答案】
(1)解:设2014至2016年该市投入科研经费的年平均增长率为x,
根据题意,得:500(1+x)2=720,
解得:x1=0.2=20%,x2=﹣2.2(舍),
答:2014至2016年该市投入科研经费的年平均增长率为20%.
(2)解:根据题意,得: ![]() ×100%≤15%,
×100%≤15%,
解得:a≤828,
又∵该市计划2017年投入的科研经费比2016年有所增加
故a的取值范围为720<a≤828.
【解析】考查一元二次方程的应用及不等式的引用;求平均变化率的方法为:若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.(1)等量关系为:2014年投入科研经费×(1+增长率)2=2016年投入科研经费,把相关数值代入求解即可;(2)根据: ![]() ×100%≤15%解不等式求解即可.
×100%≤15%解不等式求解即可.
【考点精析】认真审题,首先需要了解一元一次不等式组的应用(1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,AB=AC,∠C=70°,△AB′C′与△ABC 关于直线 EF对称,∠CAF=10°,连接 BB′,则∠ABB′的度数是( )

A. 30° B. 35° C. 40° D. 45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为24厘米.甲、乙两动点同时从顶点A出发,甲以2厘米/秒的速度沿正方形的边按顺时针方向移动,乙以4厘米/秒的速度沿正方形的边按逆时针方向移动,每次相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动,则第四次相遇时甲与最近顶点的距离是______厘米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠B=30°,∠ACB=90°,CD⊥AB交AB于D,以CD为较短的直角边向△CDB的同侧作Rt△DEC,满足∠E=30°,∠DCE=90°,再用同样的方法作Rt△FGC,∠FCG=90°,继续用同样的方法作Rt△HIC,∠HCI=90°.若AC=a,求CI的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有一张三角形纸片ABC,∠A=80°,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两张纸片均为等腰三角形,则∠C的度数可以是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,满足y的值随x的值增大而增大的是( )
A.y=﹣2x
B.y=3x﹣1
C.y=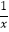
D.y=x2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.

(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
相关试题

