【题目】如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于点B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,若tan∠ABO= ![]() ,OB=4,OE=2,点D的坐标为(6,m).
,OB=4,OE=2,点D的坐标为(6,m). 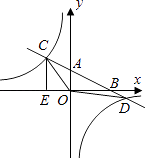
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
参考答案:
【答案】
(1)解:∵在直角△BCE中,tan∠ABO= ![]() =
= ![]() ,BE=OE+OB=4+2=6,
,BE=OE+OB=4+2=6,
∴EC=BEtan∠ABO=6× ![]() =3.
=3.
∴C的坐标是(﹣2,3).
设反比例函数的解析式是y= ![]() .
.
把C的坐标代入得:3= ![]() ,
,
解得:k=﹣6,
则反比例函数的解析式是:y=﹣ ![]()
B的坐标是(4,0).
∵在直角△AOB中,tan∠ABO= ![]() =
= ![]() ,
,
∴OA=OBtan∠ABO=4× ![]() =2,
=2,
则A的坐标是(0,2),
设直线AB的解析式是y=kx+b,
根据题意得: ![]() ,
,
解得: 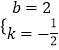 .
.
则直线AB的解析式是:y=﹣ ![]() x+2
x+2
(2)解:解方程组: 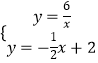 ,
,
解得: ![]() 或
或 ![]() ,
,
则D的坐标是:(6,﹣1).
∵OA=2
∴S△COD=S△OAC+S△OAD= ![]() ×2×2+
×2×2+ ![]() ×2×6=2+6=8
×2×6=2+6=8
【解析】(1)在直角△BCE中,BE=6,利用三角函数即可求得CE的长,则C的坐标即可求解,然后利用待定系数法即可求得反比例函数的解析式;(2)在直角△ABO中,利用三角函数即可求得OA的长,则A,B的坐标已知,利用待定系数法即可求得直线的解析式;(3)首先求得D的坐标,根据S△COD=S△OAC+S△OAD即可求解.
【考点精析】认真审题,首先需要了解解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(x+1)2﹣x(1﹣x)﹣2x2
(2) ÷(
÷(  ﹣a﹣b)
﹣a﹣b) -
科目: 来源: 题型:
查看答案和解析>>【题目】万州某运输公司的一艘轮船在长江上航行,往返于万州、朝天门两地。假设轮船在静水中的速度不变,长江的水流速度不变,该轮船从万州出发,逆水航行到朝天门,停留一段时间(卸货、装货、加燃料等,)又顺水航行返回万州,若该轮船从万州出发后所用时间为x(小时),轮船距万州的距离为y(千米),则下列各图中,能反映y与x之间函数关系的图象大致是【 】
A.
 B.
B.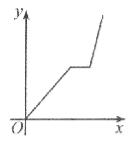 C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图①由4根火柴棍围成;图②由12根火柴棍围成;图③由24根火柴棍围成;…按此规律,则第⑥个图形由( )根火柴棍围成.
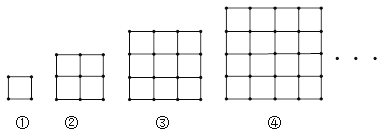
A. 60 B. 72 C. 84 D. 112
-
科目: 来源: 题型:
查看答案和解析>>【题目】每逢金秋送爽之时,正是大闸蟹上市的旺季,也是吃蟹的最好时机,可谓膏肥黄美.九月份,某经销商购进一批雌蟹、雄蟹共1000只,进价均为每只40元,然后以雌蟹每只75元、雄蟹每只60元的价格售完,共获利29000元.
(1)求该经销商分别购进雌蟹、雄蟹各多少只?
(2)民间有“九雌十雄”的说法,即九月吃雌蟹,十月吃雄蟹.十月份,在进价不变的情况下该经销商决定调整价格,将雌蟹的价格在九月份的基础上下调a%(降价后售价不低于进价),雄蟹的价格上涨 a%,同时雌蟹的销量较九月下降了
a%,同时雌蟹的销量较九月下降了  a%,雄蟹的销量上升了25%,结果十月份的销售额比九月份增加了1000元,求a的值.
a%,雄蟹的销量上升了25%,结果十月份的销售额比九月份增加了1000元,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一艘载重480 t的船,容积是1050 m3,现有甲种货物450 m3,乙种货物350 t,而甲种货物每吨体积2.5 m3,乙种货物每立方米0.5 t.问两种货物是否都能装上船? 如果不能,请说明理由,并求出为了最大限度地利用船的载重量和容积,两种货物应各装多少吨.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时
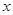 张用A方法,其余用B方法。
张用A方法,其余用B方法。(1)用
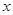 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
相关试题

